Question Number 189861 by Rupesh123 last updated on 23/Mar/23
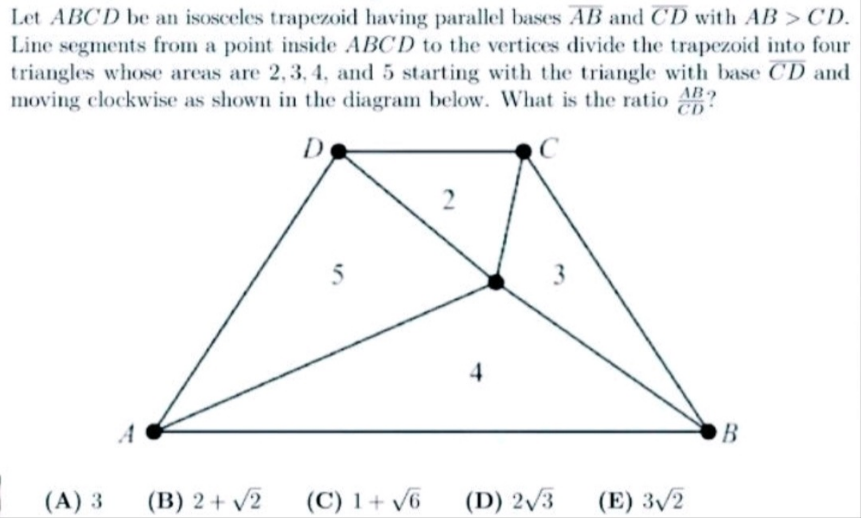
Answered by mr W last updated on 23/Mar/23

Commented by mr W last updated on 23/Mar/23

$${A}=\mathrm{2} \\ $$$${B}=\mathrm{4} \\ $$$${C}=\mathrm{5} \\ $$$${D}=\mathrm{3} \\ $$$${A}=\frac{{pa}}{\mathrm{2}}\:\Rightarrow{a}=\frac{\mathrm{2}{A}}{{p}} \\ $$$${B}=\frac{{qb}}{\mathrm{2}}\:\Rightarrow{b}=\frac{\mathrm{2}{B}}{{q}} \\ $$$${C}=\frac{\left({a}+{b}\right){c}}{\mathrm{2}}\:\Rightarrow{c}=\frac{\mathrm{2}{C}}{{a}+{b}} \\ $$$${D}=\frac{\left({a}+{b}\right){d}}{\mathrm{2}}\:\Rightarrow{d}=\frac{\mathrm{2}{D}}{{a}+{b}} \\ $$$$\frac{{c}+{d}−{p}}{{a}}=\frac{{q}−\left({c}+{d}\right)}{{b}} \\ $$$$\left({c}+{d}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)=\frac{{p}}{{a}}+\frac{{q}}{{b}} \\ $$$$\left(\frac{\mathrm{2}{C}+\mathrm{2}{D}}{{a}+{b}}\right)\left(\frac{{a}+{b}}{{ab}}\right)=\frac{{aq}+{pb}}{{ab}} \\ $$$$\mathrm{2}\left({C}+{D}\right)=\frac{\mathrm{2}{Aq}}{{p}}+\frac{\mathrm{2}{Bp}}{{q}} \\ $$$${C}+{D}=\frac{{Aq}}{{p}}+\frac{{Bp}}{{q}} \\ $$$${let}\:\lambda=\frac{{q}}{{p}} \\ $$$${A}\lambda+\frac{{B}}{\lambda}−\left({C}+{D}\right)=\mathrm{0} \\ $$$${A}\lambda^{\mathrm{2}} −\left({C}+{D}\right)\lambda+{B}=\mathrm{0} \\ $$$$\lambda=\frac{{C}+{D}\pm\sqrt{\left({C}+{D}\right)^{\mathrm{2}} −\mathrm{4}{AB}}}{\mathrm{2}{A}} \\ $$$$\lambda=\frac{\mathrm{8}\pm\sqrt{\mathrm{8}^{\mathrm{2}} −\mathrm{4}×\mathrm{8}}}{\mathrm{2}×\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{2}} \\ $$$${since}\:{given}\:{AB}>{CD},\:\Rightarrow\lambda=\mathrm{2}+\sqrt{\mathrm{2}}\:\checkmark \\ $$
Commented by Rupesh123 last updated on 23/Mar/23
Perfect ��
