Question Number 189971 by Rupesh123 last updated on 25/Mar/23
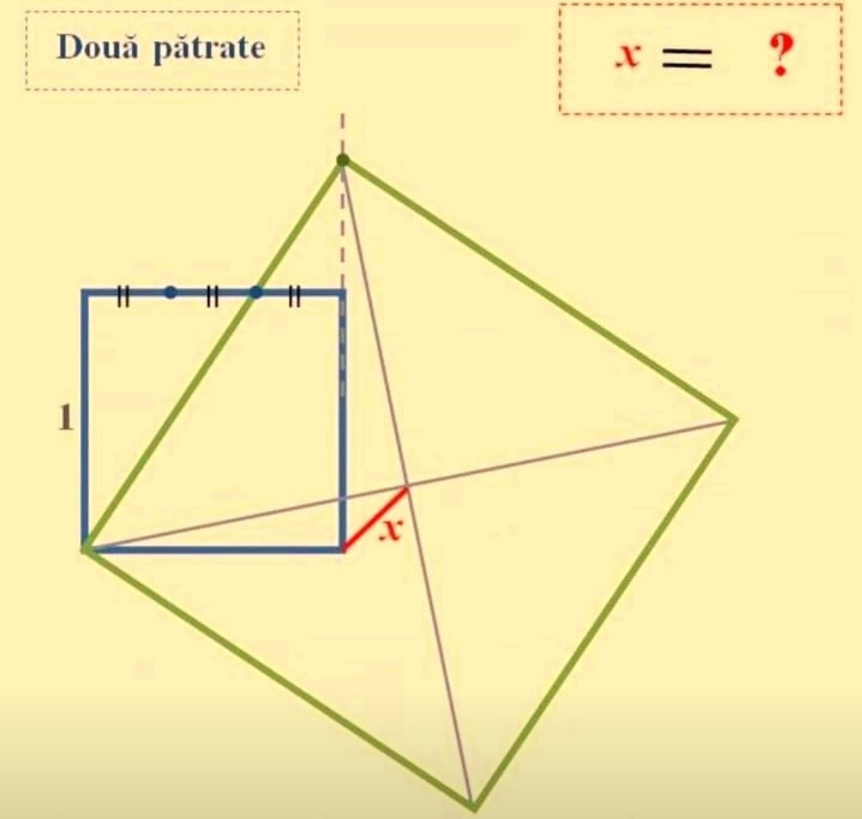
Answered by ajfour last updated on 25/Mar/23

$${y}=\frac{\mathrm{3}}{\mathrm{2}}{x} \\ $$$${s}=\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{{s}}{\:\sqrt{\mathrm{2}}}\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}} \\ $$$${q}=\frac{\mathrm{3}}{\mathrm{4}}−\frac{{s}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}\:\theta=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${p}=\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{4}}\:\:\:\:\:\:\:{q}=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} =\left(\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{4}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\:\:=\frac{\mathrm{18}+\mathrm{4}−\mathrm{12}\sqrt{\mathrm{2}}+\mathrm{9}+\mathrm{8}−\mathrm{12}\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$$\:\:=\frac{\mathrm{39}−\mathrm{24}\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$${x}=\frac{\sqrt{\mathrm{39}−\mathrm{24}\sqrt{\mathrm{2}}}}{\mathrm{4}} \\ $$$$ \\ $$
