Menu Close

Question-190644

Tinku Tara 0 Comments
Pin




Question Number 190644 by cherokeesay last updated on 08/Apr/23
Answered by a.lgnaoui last updated on 09/Apr/23
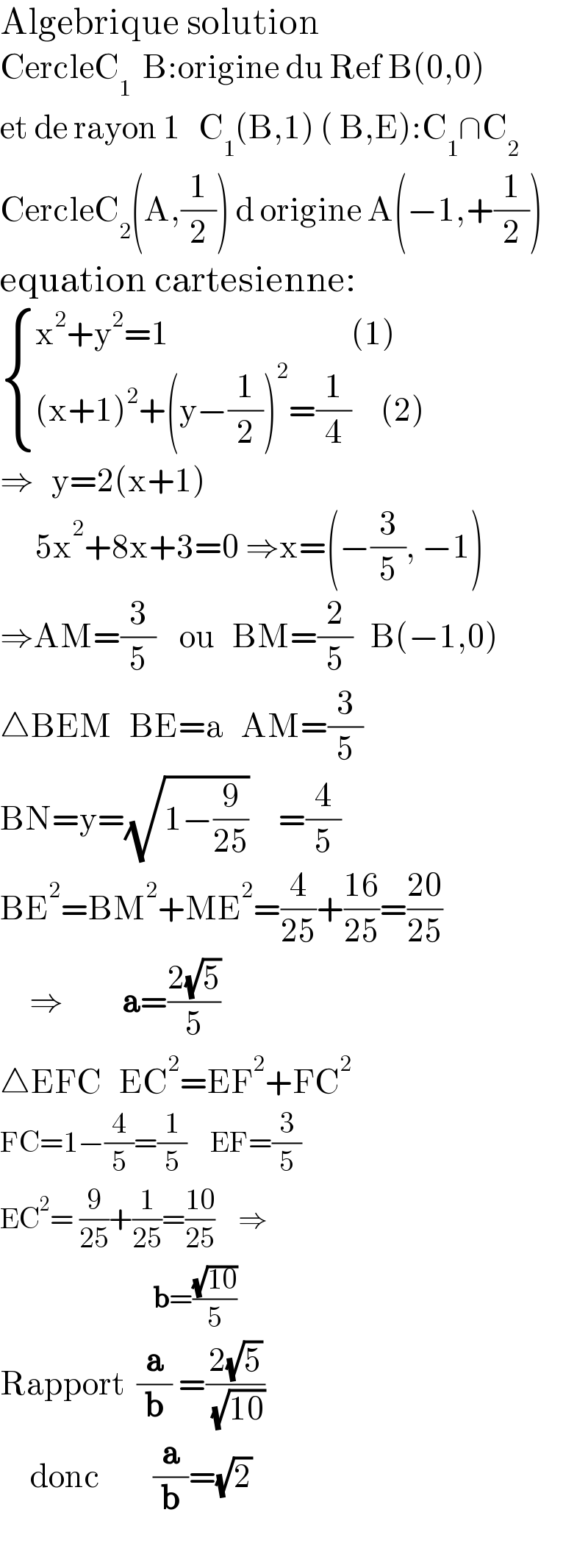
Algebrique solution CercleC_1 B:origine du Ref B(0,0) et de rayon 1 C_1 (B,1) ( B,E):C_1 ∩C_2 CercleC_2 (A,(1/2)) d origine A(−1,+(1/2)) equation cartesienne: { ((x^2 +y^2 =1 (1))),(((x+1)^2 +(y−(1/2))^2 =(1/4) (2))) :} ⇒ y=2(x+1) 5x^2 +8x+3=0 ⇒x=(−(3/5), −1) ⇒AM=(3/5) ou BM=(2/5) B(−1,0) △BEM BE=a AM=(3/5) BN=y=(√(1−(9/(25)))) =(4/5) BE^2 =BM^2 +ME^2 =(4/(25))+((16)/(25))=((20)/(25)) ⇒ a=((2(√5))/5) △EFC EC^2 =EF^2 +FC^2 FC=1−(4/5)=(1/5) EF=(3/5) EC^2 = (9/(25))+(1/(25))=((10)/(25)) ⇒ b=((√(10))/5) Rapport (a/b) =((2(√5))/( (√(10)))) donc (a/b)=(√2)
$$\mathrm{Algebrique}\:\mathrm{solution} \\ $$$$\mathrm{CercleC}_{\mathrm{1}} \:\:\mathrm{B}:\mathrm{origine}\:\mathrm{du}\:\mathrm{Ref}\:\mathrm{B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{et}\:\mathrm{de}\:\mathrm{rayon}\:\mathrm{1}\:\:\:\mathrm{C}_{\mathrm{1}} \left(\mathrm{B},\mathrm{1}\right)\:\left(\:\mathrm{B},\mathrm{E}\right):\mathrm{C}_{\mathrm{1}} \cap\mathrm{C}_{\mathrm{2}} \\ $$$$\mathrm{CercleC}_{\mathrm{2}} \left(\mathrm{A},\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{d}\:\mathrm{origine}\:\mathrm{A}\left(−\mathrm{1},+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{equation}\:\mathrm{cartesienne}: \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right)}\\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\Rightarrow\:\:\:\mathrm{y}=\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\mathrm{5x}^{\mathrm{2}} +\mathrm{8x}+\mathrm{3}=\mathrm{0}\:\Rightarrow\mathrm{x}=\left(−\frac{\mathrm{3}}{\mathrm{5}},\:−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{AM}=\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\mathrm{ou}\:\:\:\mathrm{BM}=\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\mathrm{B}\left(−\mathrm{1},\mathrm{0}\right) \\ $$$$\bigtriangleup\mathrm{BEM}\:\:\:\mathrm{BE}=\mathrm{a}\:\:\:\mathrm{AM}=\frac{\mathrm{3}}{\mathrm{5}}\:\: \\ $$$$\mathrm{BN}=\mathrm{y}=\sqrt{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{25}}}\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{5}}\:\: \\ $$$$\mathrm{BE}^{\mathrm{2}} =\mathrm{BM}^{\mathrm{2}} +\mathrm{ME}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{25}}+\frac{\mathrm{16}}{\mathrm{25}}=\frac{\mathrm{20}}{\mathrm{25}} \\ $$$$\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{a}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\bigtriangleup\mathrm{EFC}\:\:\:\mathrm{EC}^{\mathrm{2}} =\mathrm{EF}^{\mathrm{2}} +\mathrm{FC}^{\mathrm{2}} \\ $$$$\mathrm{FC}=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\mathrm{EF}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{EC}^{\mathrm{2}} =\:\frac{\mathrm{9}}{\mathrm{25}}+\frac{\mathrm{1}}{\mathrm{25}}=\frac{\mathrm{10}}{\mathrm{25}}\:\:\:\:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}=\frac{\sqrt{\mathrm{10}}}{\mathrm{5}} \\ $$$$\mathrm{Rapport}\:\:\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{b}}}\:=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{10}}} \\ $$$$\:\:\:\:\:\mathrm{donc}\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{b}}}=\sqrt{\mathrm{2}} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 09/Apr/23
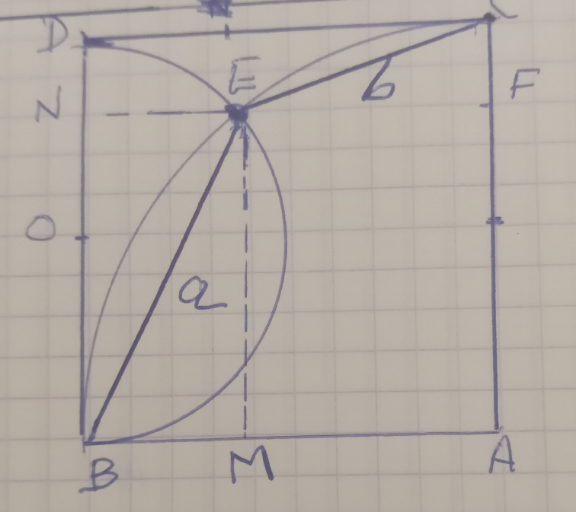
Commented by cherokeesay last updated on 09/Apr/23
Nice ! thank you sir.
$${Nice}\:!\:{thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *