Question Number 191128 by Mingma last updated on 18/Apr/23
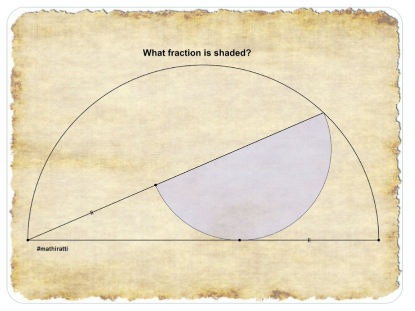
Answered by mr W last updated on 18/Apr/23

Commented by mr W last updated on 19/Apr/23

$${b}=\sqrt{\left({a}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{a}\left({a}+\mathrm{2}{r}\right)} \\ $$$$\frac{{b}}{{a}+{r}}=\frac{{a}+\mathrm{2}{r}}{{b}+{a}} \\ $$$${b}\left({b}+{a}\right)=\left({a}+{r}\right)\left({a}+\mathrm{2}{r}\right) \\ $$$${a}^{\mathrm{3}} −{r}^{\mathrm{2}} {a}−\mathrm{2}{r}^{\mathrm{3}} =\mathrm{0} \\ $$$${let}\:\lambda=\frac{{a}}{{r}} \\ $$$$\lambda^{\mathrm{3}} −\lambda−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{78}}}{\mathrm{9}}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{78}}}{\mathrm{9}}−\mathrm{1}} \\ $$$${R}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\frac{{r}}{{R}}=\frac{\mathrm{2}{r}}{{a}+{b}}=\frac{\mathrm{2}}{\lambda+\sqrt{\lambda\left(\lambda+\mathrm{2}\right)}}\approx\mathrm{0}.\mathrm{52138} \\ $$
Commented by Mingma last updated on 19/Apr/23
please check your solution well. the final answer should be 0.27
Commented by mr W last updated on 19/Apr/23

$${i}\:{have}\:{expected}\:{more}\:{care}\:{from}\:{you}. \\ $$$${are}\:{you}\:{really}\:{only}\:{interested}\:{in}\:{the} \\ $$$${final}\:{value},\:{not}\:{what}\:{the}\:{value}\:{means} \\ $$$${and}\:{how}\:{the}\:{value}\:{was}\:{obtained}? \\ $$$${i}\:{got}\:\frac{{r}}{{R}}\approx\mathrm{0}.\mathrm{52138}\:{and}\:{i}\:{didn}'{t}\:{say}\:{that} \\ $$$${this}\:{is}\:{the}\:{fraction}\:{of}\:{the}\:{shaded} \\ $$$${area}.\:{the}\:{fraction}\:{of}\:{shaded}\:{area} \\ $$$${is}\:{certainly}\:\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} \approx\mathrm{0}.\mathrm{2718}. \\ $$
Commented by Mingma last updated on 19/Apr/23
Clearly, you're right!
Thank you, sir!
