Question Number 191143 by Mingma last updated on 19/Apr/23
Answered by HeferH last updated on 21/Apr/23

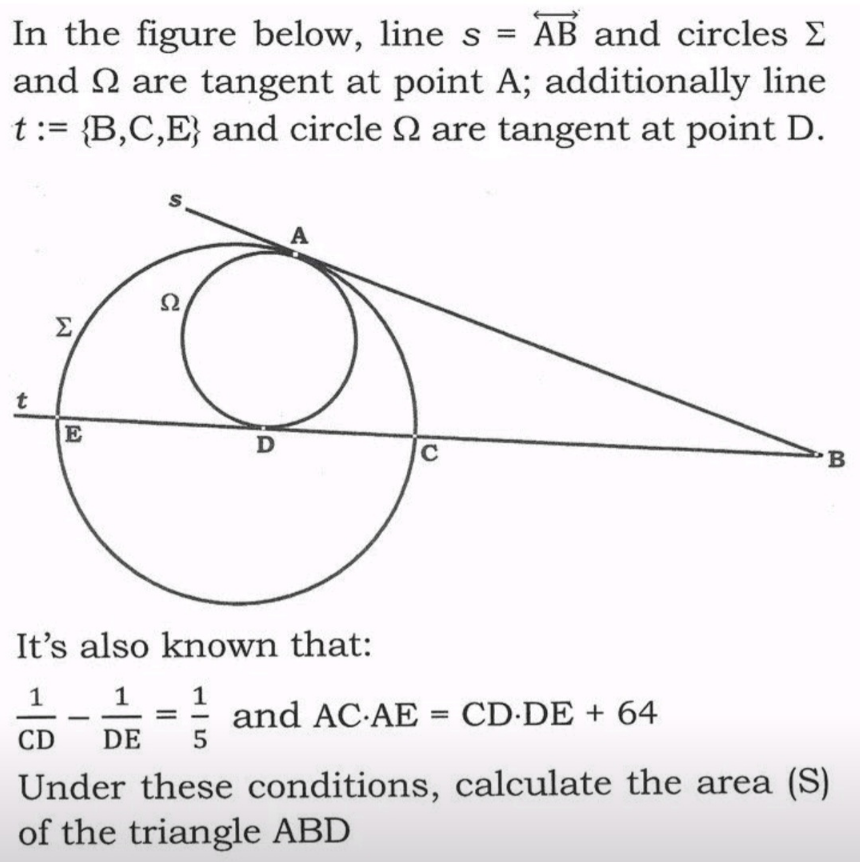
$$\mathrm{Say}\:\mathrm{CD}\:=\:\mathrm{a},\:\mathrm{DE}\:=\:\mathrm{b},\:\mathrm{AC}\:=\:\mathrm{c},\:\mathrm{AE}\:=\:\mathrm{d} \\ $$$$\:\ast\:\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\Rightarrow \\ $$$$\:\mathrm{5}\left(\mathrm{b}−\mathrm{a}\right)=\:\mathrm{ab} \\ $$$$\:\ast\:\mathrm{cd}\:=\:\mathrm{ab}+\mathrm{64} \\ $$$$\:\mathrm{Since}\:\mathrm{AD}\:\mathrm{is}\:\mathrm{bisector}: \\ $$$$\:\mathrm{AD}^{\mathrm{2}} =\:\mathrm{cd}\:−\:\mathrm{ab} \\ $$$$\:\mathrm{AD}^{\mathrm{2}} \:=\:\left(\mathrm{ab}+\mathrm{64}\right)−\mathrm{ab}\:=\:\mathrm{64} \\ $$$$\:\mathrm{AD}\:=\:\mathrm{8}\: \\ $$$$\: \\ $$$$\:\mathrm{Also}:\: \\ $$$$\:\mathrm{AB}^{\mathrm{2}} \:=\:\left(\mathrm{AB}\:+\mathrm{b}\right)\left(\mathrm{AB}−\mathrm{a}\right) \\ $$$$\:\mathrm{AB}^{\mathrm{2}} =\:\mathrm{AB}^{\mathrm{2}} −\mathrm{AB}\:\centerdot\:\mathrm{a}\:+\:\mathrm{AB}\:\centerdot\:\mathrm{b}\:−\mathrm{ab} \\ $$$$\:\mathrm{ab}\:=\:\mathrm{AB}\left(\mathrm{b}\:−\:\mathrm{a}\right) \\ $$$$\: \\ $$$$\:\mathrm{but}\::\:\:\mathrm{ab}\:=\:\mathrm{5}\left(\mathrm{b}−\mathrm{a}\right)\:\Rightarrow \\ $$$$\:\mathrm{AB}\:=\:\mathrm{5}\:=\:\mathrm{DB} \\ $$$$\:\therefore\:\mathrm{Area}\:=\:\sqrt{\mathrm{9}\left(\mathrm{9}−\mathrm{5}\right)\left(\mathrm{9}−\mathrm{5}\right)\left(\mathrm{9}−\mathrm{8}\right)}\:=\:\mathrm{3}×\mathrm{4}\:=\mathrm{12}\:\mathrm{u}^{\mathrm{2}} \\ $$
