Question Number 191335 by Mingma last updated on 23/Apr/23
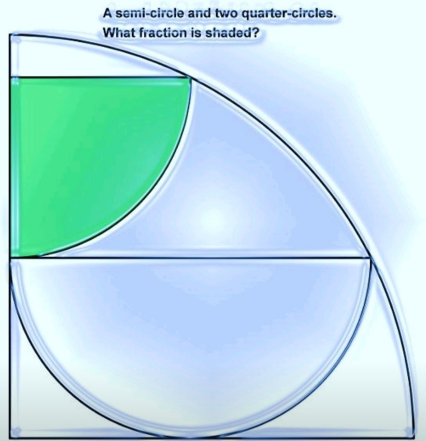
Answered by mr W last updated on 23/Apr/23

$${radius}\:{of}\:{big}\:{quatercircle}\:={a} \\ $$$${radius}\:{of}\:{big}\:{semicircle}\:={b} \\ $$$${radius}\:{of}\:{small}\:{quatercircle}\:={c} \\ $$$${b}^{\mathrm{2}} +\left(\mathrm{2}{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \:\Rightarrow{b}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{5}} \\ $$$${c}^{\mathrm{2}} +\left({c}+{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{2}{c}^{\mathrm{2}} +\mathrm{2}{bc}+{b}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{2}{c}^{\mathrm{2}} +\mathrm{2}\frac{{a}}{\:\sqrt{\mathrm{5}}}{c}+\frac{{a}^{\mathrm{2}} }{\mathrm{5}}={a}^{\mathrm{2}} \\ $$$$\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\frac{{c}}{{a}}\right)−\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{c}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{4}×\mathrm{2}}{\mathrm{5}}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${fraction}\:{of}\:{shaded}\:{area}: \\ $$$$\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{5}} \\ $$
