Question-191457

Question Number 191457 by Mingma last updated on 24/Apr/23

Commented by Tinku Tara last updated on 24/Apr/23

The user is blocked from making further posts.

$$\mathrm{The}\:\mathrm{user}\:\mathrm{is}\:\mathrm{blocked}\:\mathrm{from}\:\mathrm{making}\:\mathrm{further} \\ $$$$\mathrm{posts}. \\ $$

Commented by mr W last updated on 24/Apr/23

$${to}\:{mkaiajsk}: \\ $$$${you}\:{are}\:{disturbing}!\:{if}\:{you}\:{don}'{t}\:{like} \\ $$$${this}\:{forum},\:{you}\:{may}\:{select}\:{leaving} \\ $$$${here}.\:{please}\:{respect}\:{other}\:{people}! \\ $$

Commented by mehdee42 last updated on 24/Apr/23

$${tht}'{s}\:\:{wright} \\ $$

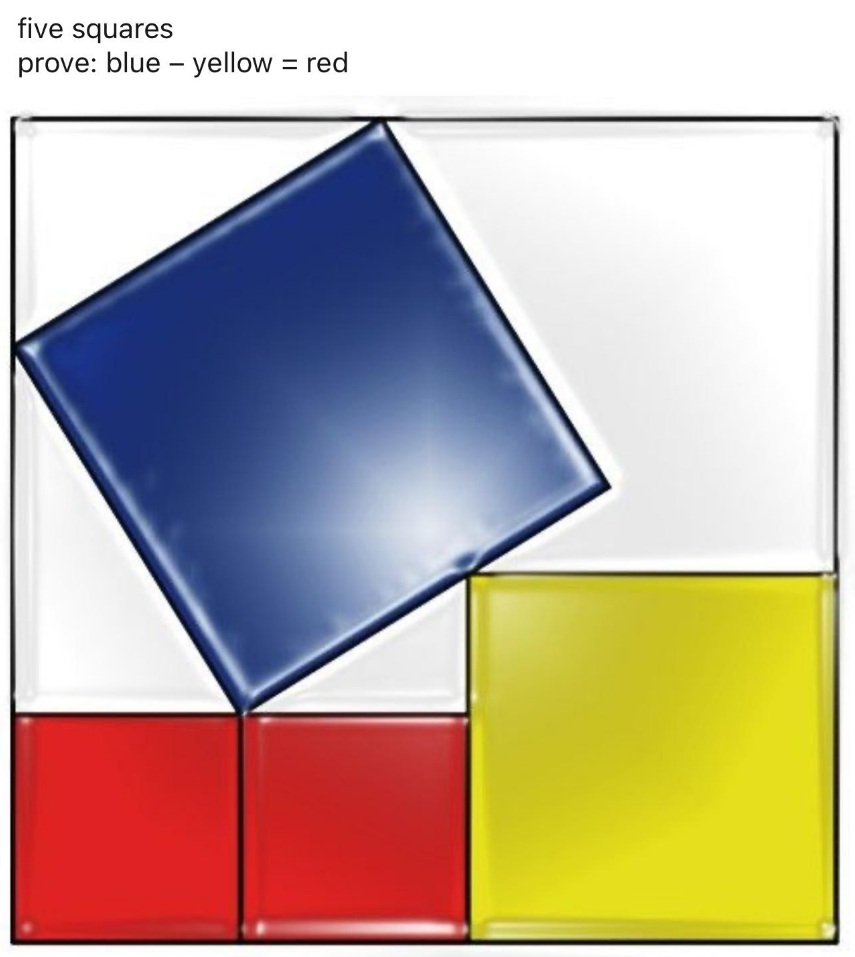
Answered by a.lgnaoui last updated on 27/Apr/23

posons: X=HF; Y=((EH)/2)=CP; Z=MN ∡PMC=∡GPD =∡ANM=θ sin θ=((PC)/(MN)) =(Y/Z) ⇒Y=Zsin θ AE=Z(cos θ+sin θ) EF=2Y+X [AEFB] Carre ⇒AE=EF Z(cos θ+sin θ)=X+2Y Zcos θ+Y=X+2Y ⇒X=Zcos θ { ((Zcos θ=X)),((Zsin θ=Y)) :} X^2 +Y^2 =Z^2 ⇒ Y^2 =Z^2 −X^2 Y^2 =Aire care Rouge Z^2 =Aire care Bleu X^2 =Aire care Jaune

$$\mathrm{posons}:\:\boldsymbol{\mathrm{X}}=\boldsymbol{\mathrm{HF}};\:\:\boldsymbol{\mathrm{Y}}=\frac{\boldsymbol{\mathrm{EH}}}{\mathrm{2}}=\boldsymbol{\mathrm{CP}};\:\:\boldsymbol{\mathrm{Z}}=\boldsymbol{\mathrm{MN}} \\ $$$$\measuredangle\mathrm{PMC}=\measuredangle\mathrm{GPD}\:\:=\measuredangle\mathrm{ANM}=\theta \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{PC}}{\mathrm{MN}}\:\:=\frac{\mathrm{Y}}{\mathrm{Z}}\:\:\:\Rightarrow\mathrm{Y}=\mathrm{Zsin}\:\theta \\ $$$$\mathrm{AE}=\mathrm{Z}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\:\:\:\mathrm{EF}=\mathrm{2Y}+\mathrm{X} \\ $$$$\left[\mathrm{AEFB}\right]\:\:\mathrm{Carre}\:\Rightarrow\mathrm{AE}=\mathrm{EF} \\ $$$$\mathrm{Z}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)=\mathrm{X}+\mathrm{2Y} \\ $$$$\mathrm{Zcos}\:\theta+\mathrm{Y}=\mathrm{X}+\mathrm{2Y}\:\Rightarrow\mathrm{X}=\mathrm{Zcos}\:\theta \\ $$$$\begin{cases}{\mathrm{Zcos}\:\theta=\mathrm{X}}\\{\mathrm{Zsin}\:\theta=\mathrm{Y}}\end{cases} \\ $$$$\mathrm{X}^{\mathrm{2}} +\mathrm{Y}^{\mathrm{2}} =\mathrm{Z}^{\mathrm{2}} \:\:\:\:\:\Rightarrow \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{Y}}^{\mathrm{2}} =\boldsymbol{\mathrm{Z}}^{\mathrm{2}} −\boldsymbol{\mathrm{X}}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Y}^{\mathrm{2}} =\mathrm{Aire}\:\mathrm{care}\:\mathrm{Rouge} \\ $$$$\mathrm{Z}^{\mathrm{2}} =\mathrm{Aire}\:\mathrm{care}\:\:\mathrm{Bleu} \\ $$$$\mathrm{X}^{\mathrm{2}} =\mathrm{Aire}\:\mathrm{care}\:\mathrm{Jaune} \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 28/Apr/23

Answered by mr W last updated on 28/Apr/23

Commented by mr W last updated on 28/Apr/23

a+(√(c^2 −a^2 ))+a=2a+b ⇒(√(c^2 −a^2 ))=b ⇒c^2 −a^2 =b^2 ⇒c^2 −b^2 =a^2 ⇒blue square−yellow square=red square

$${a}+\sqrt{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }+{a}=\mathrm{2}{a}+{b} \\ $$$$\Rightarrow\sqrt{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }={b} \\ $$$$\Rightarrow{c}^{\mathrm{2}} −{a}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} −{b}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow{blue}\:{square}−{yellow}\:{square}={red}\:{square} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply