Menu Close

Question-191756

Tinku Tara 0 Comments
Pin




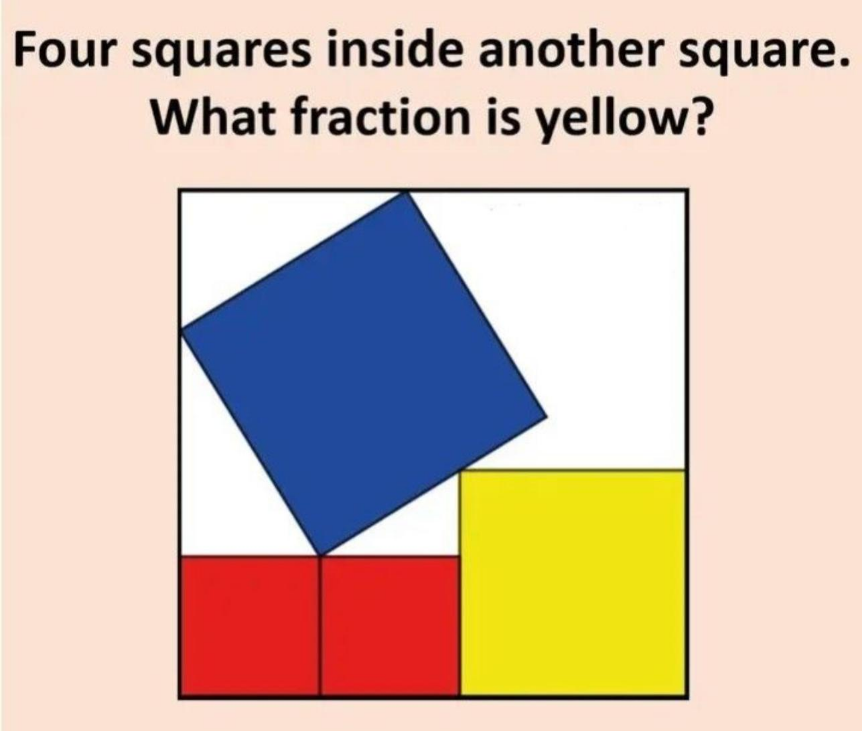
Question Number 191756 by Shlock last updated on 30/Apr/23
Answered by aleks041103 last updated on 30/Apr/23
side of whole square → a side blue/red/yellow square → b/r/y b^2 =r^2 +(a−2r)^2 =r^2 +y^2 there are two similar triangles (r/(y−r))=(y/r)⇒r^2 =y^2 −yr ⇒y^2 −yr−r^2 =0 y+2r=a⇒y=a−2r>0⇒r<a/2 ⇒(a−2r)^2 −(a−2r)r−r^2 =0 a^2 −4ar+4r^2 −ar+2r^2 −r^2 =0 5r^2 −5ar+a^2 =0 r=((5±(√(25−20)))/(10))a=((5±(√5))/(10))a r>0⇒r=((5−(√5))/(10))a⇒y=a(1−((5−(√5))/5))=(a/( (√5)))=y also (S_y /S_(tot) )=((y/a))^2 =(1/5)=(S_y /S_(tot) )
$${side}\:{of}\:{whole}\:{square}\:\rightarrow\:{a} \\ $$$${side}\:{blue}/{red}/{yellow}\:{square}\:\rightarrow\:{b}/{r}/{y} \\ $$$${b}^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({a}−\mathrm{2}{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${there}\:{are}\:{two}\:{similar}\:{triangles} \\ $$$$\frac{{r}}{{y}−{r}}=\frac{{y}}{{r}}\Rightarrow{r}^{\mathrm{2}} ={y}^{\mathrm{2}} −{yr} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −{yr}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${y}+\mathrm{2}{r}={a}\Rightarrow{y}={a}−\mathrm{2}{r}>\mathrm{0}\Rightarrow{r}<{a}/\mathrm{2} \\ $$$$\Rightarrow\left({a}−\mathrm{2}{r}\right)^{\mathrm{2}} −\left({a}−\mathrm{2}{r}\right){r}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}{ar}+\mathrm{4}{r}^{\mathrm{2}} −{ar}+\mathrm{2}{r}^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}{r}^{\mathrm{2}} −\mathrm{5}{ar}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${r}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{20}}}{\mathrm{10}}{a}=\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{10}}{a} \\ $$$${r}>\mathrm{0}\Rightarrow{r}=\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{10}}{a}\Rightarrow{y}={a}\left(\mathrm{1}−\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{5}}\right)=\frac{{a}}{\:\sqrt{\mathrm{5}}}={y} \\ $$$${also} \\ $$$$\frac{{S}_{{y}} }{{S}_{{tot}} }=\left(\frac{{y}}{{a}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{5}}=\frac{{S}_{{y}} }{{S}_{{tot}} } \\ $$
Commented by Shlock last updated on 30/Apr/23
Excellent!
Answered by mr W last updated on 30/Apr/23
side of red square =a side of yellow square =b side of blue square =c=(√(a^2 +b^2 )) side of big white square =d=2a+b ((b−a)/a)=(a/b) ⇒((a/b))^2 +(a/b)−1=0 ⇒(a/b)=((−1+(√5))/2) fraction of yellow square: (b^2 /d^2 )=((b/(2a+b)))^2 =((1/(2×(a/b)+1)))^2 =((1/( (√5))))^2 =(1/5)
$${side}\:{of}\:{red}\:{square}\:={a} \\ $$$${side}\:{of}\:{yellow}\:{square}\:={b} \\ $$$${side}\:{of}\:{blue}\:{square}\:={c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${side}\:{of}\:{big}\:{white}\:{square}\:={d}=\mathrm{2}{a}+{b} \\ $$$$\frac{{b}−{a}}{{a}}=\frac{{a}}{{b}} \\ $$$$\Rightarrow\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\frac{{a}}{{b}}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${fraction}\:{of}\:{yellow}\:{square}: \\ $$$$\frac{{b}^{\mathrm{2}} }{{d}^{\mathrm{2}} }=\left(\frac{{b}}{\mathrm{2}{a}+{b}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}×\frac{{a}}{{b}}+\mathrm{1}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{5}} \\ $$
Commented by Shlock last updated on 30/Apr/23
Excellent!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *