Menu Close

Question-191854

Tinku Tara 0 Comments
Pin




Question Number 191854 by Rupesh123 last updated on 01/May/23
Answered by a.lgnaoui last updated on 02/May/23
l image comporte 3 principaleSs surfaces β€’S1: Surface du quart ceecle C1 (rayonr_1 =2) β€’S2: Surface petit cercleC2(ryon :r_2 ) β€’S3:Surface portion cercle (rayon r_3 ) avec r_3 =AB=BC S_1 =((𝛑×4)/4)=𝛑 ; OF=OE+EF=OE+r_2 β‡’ 2=OE+r_2 OE^2 =2r_2 ^2 β‡’OE=r_2 (√2) β‡’ r_2 =2(√2) βˆ’2 S_2 =𝛑r_2 ^2 =4𝛑((√2)βˆ’1 )^2 ((S_1 βˆ’S_2 )/2) =A_1 +(A_2 /2) Calcul A_2 A_2 =OH^2 βˆ’(S_2 /4)=r_2 ^2 βˆ’((𝛑r_2 ^2 )/4)=(3/4)𝛑r_2 ^2 donc A_1 +A_2 =((S_1 βˆ’S_2 )/2)+(3/8)𝛑r_2 ^2 =((π›‘βˆ’4𝛑((√2)βˆ’1 )^2 )/2)+(3/8)𝛑×4((√2) βˆ’1)^2 A_1 +A_2 =((√2) βˆ’1)𝛑 β€’calcul A_3 Surface Portion arc de cercle OAC Surface( Arc de cercle BAC)βˆ’(Surface triangle OAB) β‡’Surface arc=𝛑AB^2 ((𝛉/(2Ο€)))(𝛉 en radian) r_3 =AB=2(√2) (B centre cercle C3) sin ΞΈ=cos ΞΈ=((√2)/2)β‡’ ΞΈ=(Ο€/4) S_3 =((𝛑×8)/8)=𝛑 surface triangle =((AB^2 )/2)=2 β‡’A_3 =(S_3 βˆ’4) A3=π›‘βˆ’2 Conclusion: S=A_1 +A_2 +A_3 ((√2) βˆ’1)𝛑+π›‘βˆ’2 S=𝛑(√2) βˆ’2
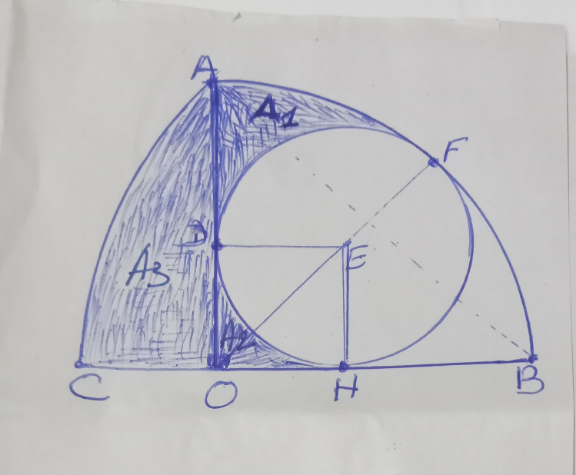
$$\mathrm{l}\:\mathrm{image}\:\mathrm{comporte}\:\mathrm{3}\:\mathrm{principale}\boldsymbol{\mathrm{S}}\mathrm{s}\:\mathrm{surfaces} \\ $$$$\bullet\boldsymbol{\mathrm{S}}\mathrm{1}:\:\:\boldsymbol{\mathrm{S}}\mathrm{urface}\:\mathrm{du}\:\mathrm{quart}\:\mathrm{ceecle}\:\mathrm{C1}\:\left(\mathrm{rayon}\boldsymbol{\mathrm{r}}_{\mathrm{1}} =\mathrm{2}\right) \\ $$$$\bullet\mathrm{S2}:\:\boldsymbol{\mathrm{S}}\mathrm{urface}\:\mathrm{petit}\:\mathrm{cercleC2}\left(\mathrm{ryon}\::\boldsymbol{\mathrm{r}}_{\mathrm{2}} \right) \\ $$$$\bullet\boldsymbol{\mathrm{S}}\mathrm{3}:\mathrm{Surface}\:\mathrm{portion}\:\mathrm{cercle}\:\left(\mathrm{rayon}\:\boldsymbol{\mathrm{r}}_{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{a}}\mathrm{vec}\:\:\mathrm{r}_{\mathrm{3}} =\boldsymbol{\mathrm{AB}}=\boldsymbol{\mathrm{BC}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{S}}_{\mathrm{1}} =\frac{\boldsymbol{\pi}Γ—\mathrm{4}}{\mathrm{4}}=\boldsymbol{\pi}\:\:;\: \\ $$$$\:\:\:\boldsymbol{\mathrm{OF}}=\boldsymbol{\mathrm{OE}}+\boldsymbol{\mathrm{EF}}=\boldsymbol{\mathrm{OE}}+\boldsymbol{\mathrm{r}}_{\mathrm{2}} \Rightarrow\:\:\mathrm{2}=\boldsymbol{\mathrm{OE}}+\boldsymbol{\mathrm{r}}_{\mathrm{2}} \\ $$$$\:\:\:\boldsymbol{\mathrm{OE}}^{\mathrm{2}} =\mathrm{2}\boldsymbol{\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} \Rightarrow\boldsymbol{\mathrm{OE}}=\boldsymbol{\mathrm{r}}_{\mathrm{2}} \sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\Rightarrow\:\:\boldsymbol{\mathrm{r}}_{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{S}}_{\mathrm{2}} =\boldsymbol{\pi\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{4}\boldsymbol{\pi}\left(\sqrt{\mathrm{2}}βˆ’\mathrm{1}\:\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\: \\ $$$$\:\:\: \\ $$$$\:\: \\ $$$$\:\frac{\boldsymbol{\mathrm{S}}_{\mathrm{1}} βˆ’\boldsymbol{\mathrm{S}}_{\mathrm{2}} }{\mathrm{2}}\:\:=\boldsymbol{\mathrm{A}}_{\mathrm{1}} +\frac{\boldsymbol{\mathrm{A}}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{Calcul}\:\:\:\boldsymbol{\mathrm{A}}_{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{A}}_{\mathrm{2}} =\boldsymbol{\mathrm{OH}}^{\mathrm{2}} βˆ’\frac{\boldsymbol{\mathrm{S}}_{\mathrm{2}} }{\mathrm{4}}=\boldsymbol{\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} βˆ’\frac{\boldsymbol{\pi\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}}\boldsymbol{\pi\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\mathrm{donc}\:\:\boldsymbol{\mathrm{A}}_{\mathrm{1}} +\boldsymbol{\mathrm{A}}_{\mathrm{2}} =\frac{\boldsymbol{\mathrm{S}}_{\mathrm{1}} βˆ’\boldsymbol{\mathrm{S}}_{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{\pi\mathrm{r}}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{\boldsymbol{\pi}βˆ’\mathrm{4}\boldsymbol{\pi}\left(\sqrt{\mathrm{2}}βˆ’\mathrm{1}\:\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{\pi}Γ—\mathrm{4}\left(\sqrt{\mathrm{2}}\:βˆ’\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{A}_{\mathrm{1}} +\mathrm{A}_{\mathrm{2}} =\left(\sqrt{\mathrm{2}}\:βˆ’\mathrm{1}\right)\boldsymbol{\pi} \\ $$$$\bullet\mathrm{calcul}\:\boldsymbol{\mathrm{A}}_{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{urface}\:\boldsymbol{\mathrm{Porti}}\mathrm{o}\boldsymbol{\mathrm{n}}\:\:\mathrm{arc}\:\mathrm{de}\:\mathrm{cercle}\:\boldsymbol{\mathrm{OAC}}\:\: \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{urface}\left(\:\mathrm{Arc}\:\mathrm{de}\:\mathrm{cercle}\:\mathrm{BAC}\right)βˆ’\left(\mathrm{Surface}\:\mathrm{triangle}\:\mathrm{OAB}\right) \\ $$$$\Rightarrow\mathrm{Surface}\:\mathrm{arc}=\boldsymbol{\pi\mathrm{AB}}^{\mathrm{2}} \left(\frac{\boldsymbol{\theta}}{\mathrm{2}\pi}\right)\left(\boldsymbol{\theta}\:\:\:\mathrm{en}\:\mathrm{radian}\right)\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{r}}_{\mathrm{3}} =\boldsymbol{\mathrm{AB}}=\mathrm{2}\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{B}}\:\mathrm{centre}\:\mathrm{cercle}\:\mathrm{C3}\right) \\ $$$$\mathrm{sin}\:\theta=\mathrm{cos}\:\theta=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\Rightarrow\:\:\:\theta=\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{S}_{\mathrm{3}} =\frac{\boldsymbol{\pi}Γ—\mathrm{8}}{\mathrm{8}}=\boldsymbol{\pi} \\ $$$$\mathrm{surface}\:\mathrm{triangle}\:=\frac{\mathrm{AB}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2} \\ $$$$\Rightarrow\boldsymbol{\mathrm{A}}_{\mathrm{3}} =\left(\boldsymbol{\mathrm{S}}_{\mathrm{3}} βˆ’\mathrm{4}\right)\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{A}}\mathrm{3}=\boldsymbol{\pi}βˆ’\mathrm{2} \\ $$$$\boldsymbol{\mathrm{Conclusion}}: \\ $$$$\:\:\:\boldsymbol{\mathrm{S}}=\boldsymbol{\mathrm{A}}_{\mathrm{1}} +\boldsymbol{\mathrm{A}}_{\mathrm{2}} +\boldsymbol{\mathrm{A}}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\left(\sqrt{\mathrm{2}}\:βˆ’\mathrm{1}\right)\boldsymbol{\pi}+\boldsymbol{\pi}βˆ’\mathrm{2}\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}=\boldsymbol{\pi}\sqrt{\mathrm{2}}\:βˆ’\mathrm{2} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 03/May/23

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *