Question Number 191958 by Rupesh123 last updated on 04/May/23
Commented by Rupesh123 last updated on 04/May/23
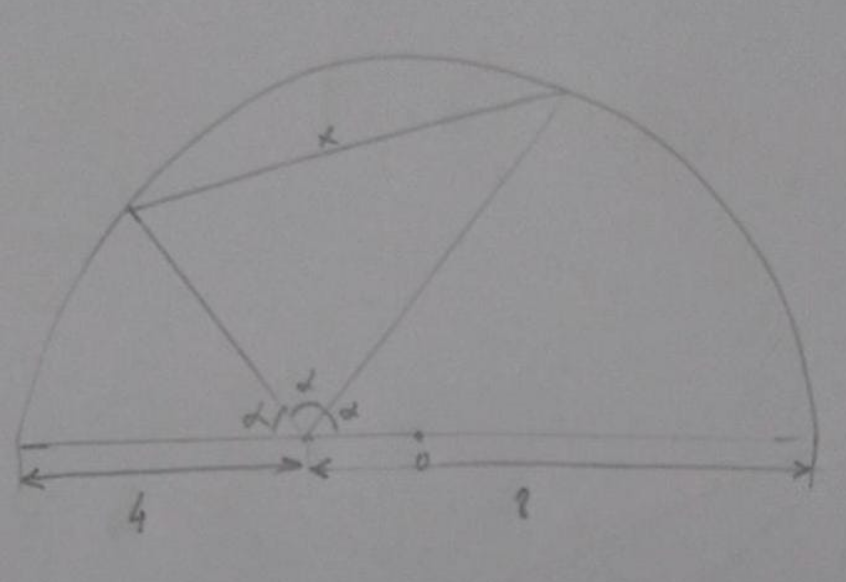
x=?
Commented by mr W last updated on 04/May/23

$${x}={r}=\frac{{a}+{b}}{\mathrm{2}}=\frac{\mathrm{4}+\mathrm{8}}{\mathrm{2}}=\mathrm{6} \\ $$
Answered by mr W last updated on 04/May/23

Commented by mr W last updated on 04/May/23

$${a}=\mathrm{4} \\ $$$${b}=\mathrm{8} \\ $$$${r}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\alpha=\frac{\pi}{\mathrm{3}} \\ $$$${OD}=\frac{{b}−{a}}{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} ={c}^{\mathrm{2}} +\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}{c}\left(\frac{{b}−{a}}{\mathrm{2}}\right)\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} +\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{c}\left(\frac{{b}−{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{c}^{\mathrm{2}} −\left(\frac{{a}−{b}}{\mathrm{2}}\right){c}−{ab}=\mathrm{0} \\ $$$${similarly} \\ $$$$\Rightarrow{d}^{\mathrm{2}} +\left(\frac{{a}−{b}}{\mathrm{2}}\right){d}−{ab}=\mathrm{0} \\ $$$${d}\:{and}\:−{c}\:{are}\:{roots}\:{of}\:{z}^{\mathrm{2}} +\left(\frac{{a}−{b}}{\mathrm{2}}\right){z}−{ab}=\mathrm{0}. \\ $$$$\Rightarrow{d}−{c}=−\frac{{a}−{b}}{\mathrm{2}} \\ $$$$\Rightarrow−{cd}=−{ab} \\ $$$${x}^{\mathrm{2}} ={c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}{cd}\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}}={c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{cd}=\left({d}−{c}\right)^{\mathrm{2}} +{cd} \\ $$$${x}^{\mathrm{2}} =\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{2}} +{ab}=\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{x}={r}=\frac{{a}+{b}}{\mathrm{2}}=\frac{\mathrm{4}+\mathrm{8}}{\mathrm{2}}=\mathrm{6} \\ $$
Commented by Shlock last updated on 04/May/23
This is perfect ��
