Question Number 19230 by tawa tawa last updated on 07/Aug/17
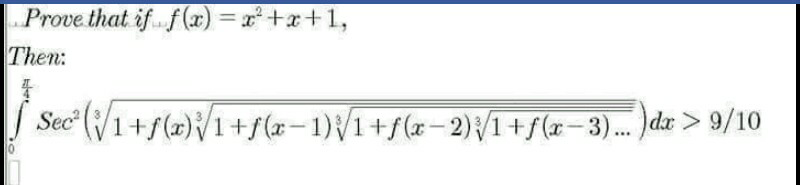
Answered by ajfour last updated on 07/Aug/17
![let g(x)=((1+f(x)((1+f(x−1)((1+f(x−2)((1+...))^(1/3) ))^(1/3) ))^(1/3) ))^(1/3) ⇒ [g(x)]^3 =1+f(x)g(x−1) ⇒ degree of g(x) is 1. let g(x)=Ax+B ⇒ (Ax+B)^3 =1+(x^2 +x+1)(Ax−A+B) comparing coefficients of x^(3 ) ,x^2 , x, and the constant term: A^3 =A ; 3A^2 B=A+B−A; 3AB^2 =B−A+A; B^3 =1+B−A ⇒ A=1, B=0 so g(x)=x ∫_0 ^( π/4) sec^2 xdx = (tan x)∣_0 ^(π/4) = 1>(9/(10)) .](https://www.tinkutara.com/question/Q19233.png)
$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{f}\left(\mathrm{x}−\mathrm{2}\right)\sqrt[{\mathrm{3}}]{\mathrm{1}+…}}}}\: \\ $$$$\Rightarrow\:\left[\mathrm{g}\left(\mathrm{x}\right)\right]^{\mathrm{3}} =\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)\mathrm{g}\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{degree}\:\mathrm{of}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{1}. \\ $$$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{Ax}+\mathrm{B} \\ $$$$\Rightarrow\:\left(\mathrm{Ax}+\mathrm{B}\right)^{\mathrm{3}} =\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\left(\mathrm{Ax}−\mathrm{A}+\mathrm{B}\right) \\ $$$$\mathrm{comparing}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}\:} ,\mathrm{x}^{\mathrm{2}} ,\:\mathrm{x}, \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{term}: \\ $$$$\mathrm{A}^{\mathrm{3}} =\mathrm{A}\:;\:\:\mathrm{3A}^{\mathrm{2}} \mathrm{B}=\mathrm{A}+\mathrm{B}−\mathrm{A}; \\ $$$$\mathrm{3AB}^{\mathrm{2}} =\mathrm{B}−\mathrm{A}+\mathrm{A};\:\:\:\mathrm{B}^{\mathrm{3}} =\mathrm{1}+\mathrm{B}−\mathrm{A} \\ $$$$\Rightarrow\:\:\mathrm{A}=\mathrm{1},\:\mathrm{B}=\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x} \\ $$$$\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{sec}\:^{\mathrm{2}} \mathrm{xdx}\:=\:\left(\mathrm{tan}\:\mathrm{x}\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} =\:\mathrm{1}>\frac{\mathrm{9}}{\mathrm{10}}\:. \\ $$
Commented by tawa tawa last updated on 07/Aug/17
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}… \\ $$
