Question-19247

Question Number 19247 by 99 last updated on 07/Aug/17

Commented by NEC last updated on 08/Aug/17

$${please}\:{type}\:{it}\:{so}\:{we}\:{can}\:{see}\:{it} \\ $$$${clearly}. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 08/Aug/17

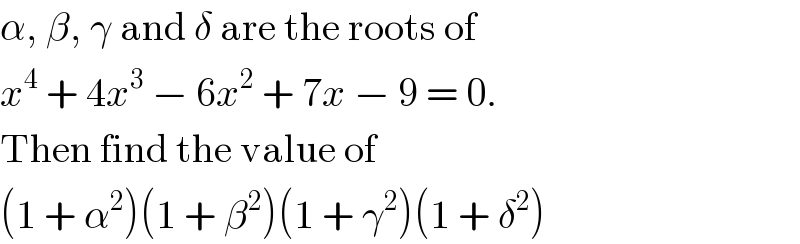
α, β, γ and δ are the roots of x^4 + 4x^3 − 6x^2 + 7x − 9 = 0. Then find the value of (1 + α^2 )(1 + β^2 )(1 + γ^2 )(1 + δ^2 )

$$\alpha,\:\beta,\:\gamma\:\mathrm{and}\:\delta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of} \\ $$$${x}^{\mathrm{4}} \:+\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{6}{x}^{\mathrm{2}} \:+\:\mathrm{7}{x}\:−\:\mathrm{9}\:=\:\mathrm{0}. \\ $$$$\mathrm{Then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\left(\mathrm{1}\:+\:\alpha^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\beta^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\gamma^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\delta^{\mathrm{2}} \right) \\ $$

Answered by Tinkutara last updated on 10/Aug/17

Since α, β, γ, δ are the roots of the given equation, we have x^4 + 4x^3 − 6x^2 + 7x − 9 = (x − α)(x − β)(x − γ)(x − δ) Putting x = i and then x = −i, we get 1 − 4i + 6 + 7i − 9 = (i − α)(i − β)(i − γ)(i − δ) and 1 + 4i + 6 − 7i − 9 = (−i − α)(−i − β)(−i − γ)(−i − δ) Multiplying these two equations, we get (−2 + 3i)(−2 − 3i) = (1 + α^2 )(1 + β^2 )(1 + γ^2 )(1 + δ^2 ) or 13 = (1 + α^2 )(1 + β^2 )(1 + γ^2 )(1 + δ^2 )

$$\mathrm{Since}\:\alpha,\:\beta,\:\gamma,\:\delta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{equation},\:\mathrm{we}\:\mathrm{have} \\ $$$${x}^{\mathrm{4}} \:+\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{6}{x}^{\mathrm{2}} \:+\:\mathrm{7}{x}\:−\:\mathrm{9}\:= \\ $$$$\left({x}\:−\:\alpha\right)\left({x}\:−\:\beta\right)\left({x}\:−\:\gamma\right)\left({x}\:−\:\delta\right) \\ $$$$\mathrm{Putting}\:{x}\:=\:{i}\:\mathrm{and}\:\mathrm{then}\:{x}\:=\:−{i},\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{1}\:−\:\mathrm{4}{i}\:+\:\mathrm{6}\:+\:\mathrm{7}{i}\:−\:\mathrm{9}\:= \\ $$$$\left({i}\:−\:\alpha\right)\left({i}\:−\:\beta\right)\left({i}\:−\:\gamma\right)\left({i}\:−\:\delta\right) \\ $$$$\mathrm{and}\:\mathrm{1}\:+\:\mathrm{4}{i}\:+\:\mathrm{6}\:−\:\mathrm{7}{i}\:−\:\mathrm{9}\:= \\ $$$$\left(−{i}\:−\:\alpha\right)\left(−{i}\:−\:\beta\right)\left(−{i}\:−\:\gamma\right)\left(−{i}\:−\:\delta\right) \\ $$$$\mathrm{Multiplying}\:\mathrm{these}\:\mathrm{two}\:\mathrm{equations},\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(−\mathrm{2}\:+\:\mathrm{3}{i}\right)\left(−\mathrm{2}\:−\:\mathrm{3}{i}\right)\:= \\ $$$$\left(\mathrm{1}\:+\:\alpha^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\beta^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\gamma^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\delta^{\mathrm{2}} \right) \\ $$$$\mathrm{or} \\ $$$$\mathrm{13}\:=\:\left(\mathrm{1}\:+\:\alpha^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\beta^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\gamma^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:\delta^{\mathrm{2}} \right) \\ $$

Commented by ajfour last updated on 10/Aug/17

$$\mathrm{how}\:\mathrm{nice}\:! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply