Question Number 192661 by Mingma last updated on 24/May/23

Commented by Mingma last updated on 24/May/23
Prove that
Commented by Mingma last updated on 25/May/23
Perfect ��
Answered by AST last updated on 24/May/23
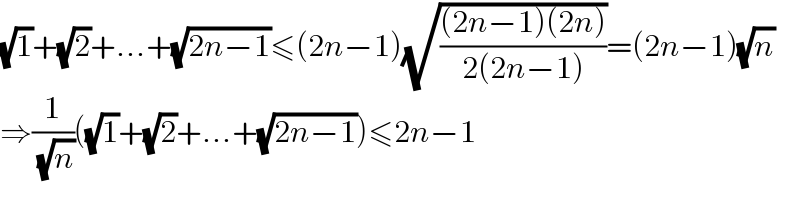
$$\sqrt{\mathrm{1}}+\sqrt{\mathrm{2}}+…+\sqrt{\mathrm{2}{n}−\mathrm{1}}\leqslant\left(\mathrm{2}{n}−\mathrm{1}\right)\sqrt{\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)}{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)}}=\left(\mathrm{2}{n}−\mathrm{1}\right)\sqrt{{n}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{n}}}\left(\sqrt{\mathrm{1}}+\sqrt{\mathrm{2}}+…+\sqrt{\mathrm{2}{n}−\mathrm{1}}\right)\leqslant\mathrm{2}{n}−\mathrm{1} \\ $$
Commented by Mingma last updated on 25/May/23
Perfect ��
