Question Number 192959 by Mingma last updated on 31/May/23
Answered by a.lgnaoui last updated on 01/Jun/23

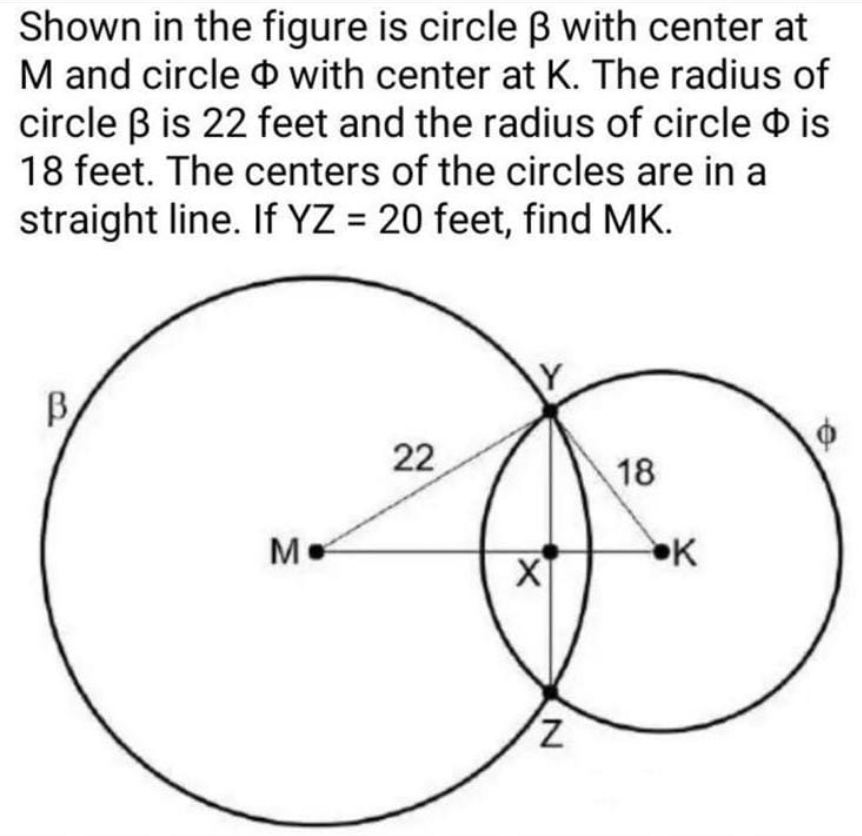
$$\bigtriangleup\mathrm{MYX}\:\mathrm{et}\:\:\mathrm{KYX}\:\:\:\mathrm{triangles}\:\mathrm{rectangles} \\ $$$$\mathrm{en}\:\mathrm{plus}\:\:\mathrm{la}\:\mathrm{corde}\:\mathrm{commun}\:\mathrm{YZ}=\mathrm{2XY} \\ $$$$\Rightarrow\:\mathrm{YX}\:=\frac{\mathrm{YZ}}{\mathrm{2}}=\mathrm{10} \\ $$$$\:\:\mathrm{MK}=\mathrm{MX}+\mathrm{XK} \\ $$$$\bigtriangleup\mathrm{MYX}\:\:\:\:\mathrm{MY}^{\mathrm{2}} =\mathrm{MX}^{\mathrm{2}} +\mathrm{XY}^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{MX}=\sqrt{\mathrm{22}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }\:=\mathrm{19},\mathrm{60} \\ $$$$\bigtriangleup\mathrm{KXY}\:\:\:\:\:\mathrm{YK}^{\mathrm{2}} =\mathrm{KX}^{\mathrm{2}} +\mathrm{XY}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{KX}=\sqrt{\mathrm{18}^{\mathrm{2}} \:−\mathrm{10}^{\mathrm{2}} }\:=\sqrt{\mathrm{384}}\:=\mathrm{15} \\ $$$$\mathrm{alors}\:\:\:\boldsymbol{\mathrm{MK}}=\boldsymbol{\mathrm{MX}}+\boldsymbol{\mathrm{XK}}=\mathrm{34},\mathrm{6} \\ $$$$ \\ $$
Commented by Mingma last updated on 01/Jun/23
Good ��
