Question Number 192966 by Mingma last updated on 01/Jun/23
Answered by aleks041103 last updated on 01/Jun/23

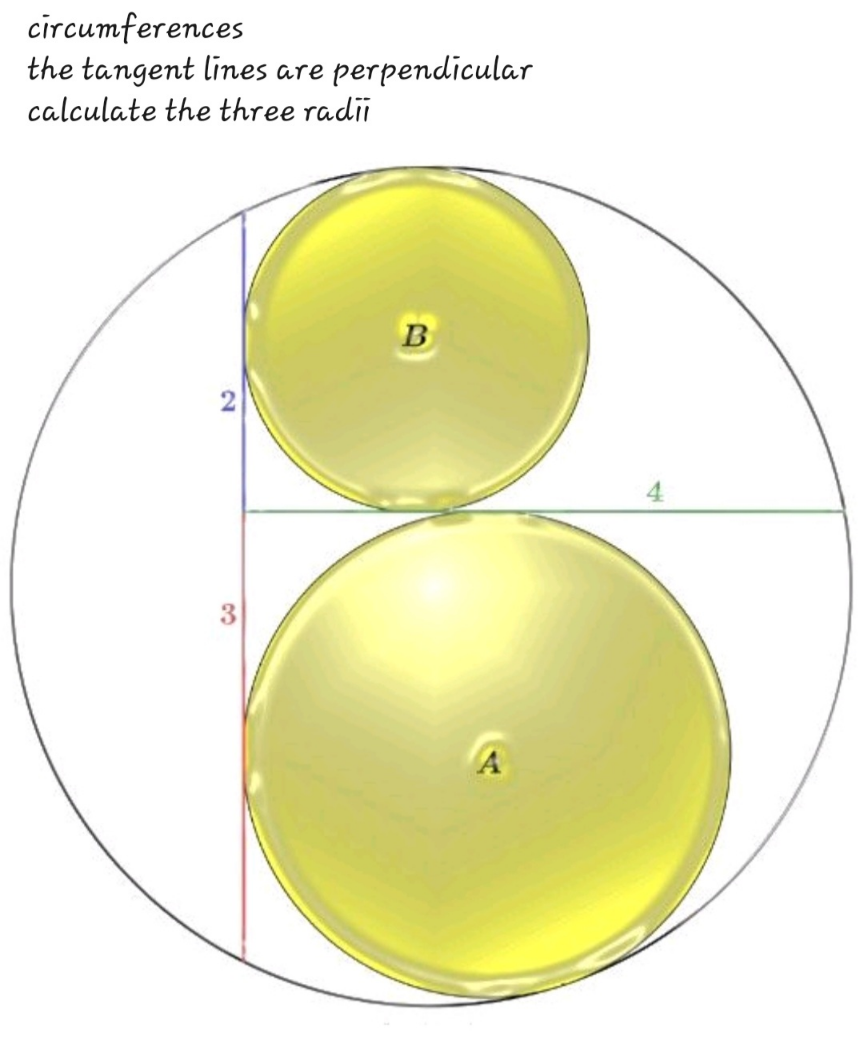
$${at}\:{the}\:{intersection}\:\left(\mathrm{0},\mathrm{0}\right)\in\mathbb{R}^{\mathrm{2}} . \\ $$$${the}\:{whole}\:{circle}\:{is} \\ $$$$\left({x}−\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{125}}{\mathrm{16}}=\left(\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$${centers}\:{of}\:{A}\:{and}\:{B}\:{lie}\:{on}\:{the}\:{angle}\:{bisectors} \\ $$$${i}.{e}.\:{center}\:{of}\:{B}\:{lies}\:{on}\:{y}={x}={R} \\ $$$$\Rightarrow\left({R}−\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} +\left({R}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}}−{R}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{R}^{\mathrm{2}} +\frac{\mathrm{29}}{\mathrm{16}}−\frac{\mathrm{3}}{\mathrm{2}}{R}=\frac{\mathrm{125}}{\mathrm{16}}+{R}^{\mathrm{2}} −\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}{R} \\ $$$${R}^{\mathrm{2}} +\frac{\mathrm{5}\sqrt{\mathrm{5}}−\mathrm{3}}{\mathrm{2}}{R}−\mathrm{6}=\mathrm{0} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\left(\frac{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{24}}\right) \\ $$$$=\frac{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{230}−\mathrm{30}\sqrt{\mathrm{5}}}= \\ $$$$=\frac{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\mathrm{15}−\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{18}−\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${R}_{{B}} =\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${for}\:{A}\:{the}\:{same}. \\ $$$${you}\:{can}\:{do}\:{the}\:{rest}. \\ $$$$ \\ $$
Commented by Mingma last updated on 01/Jun/23
Perfect ��
