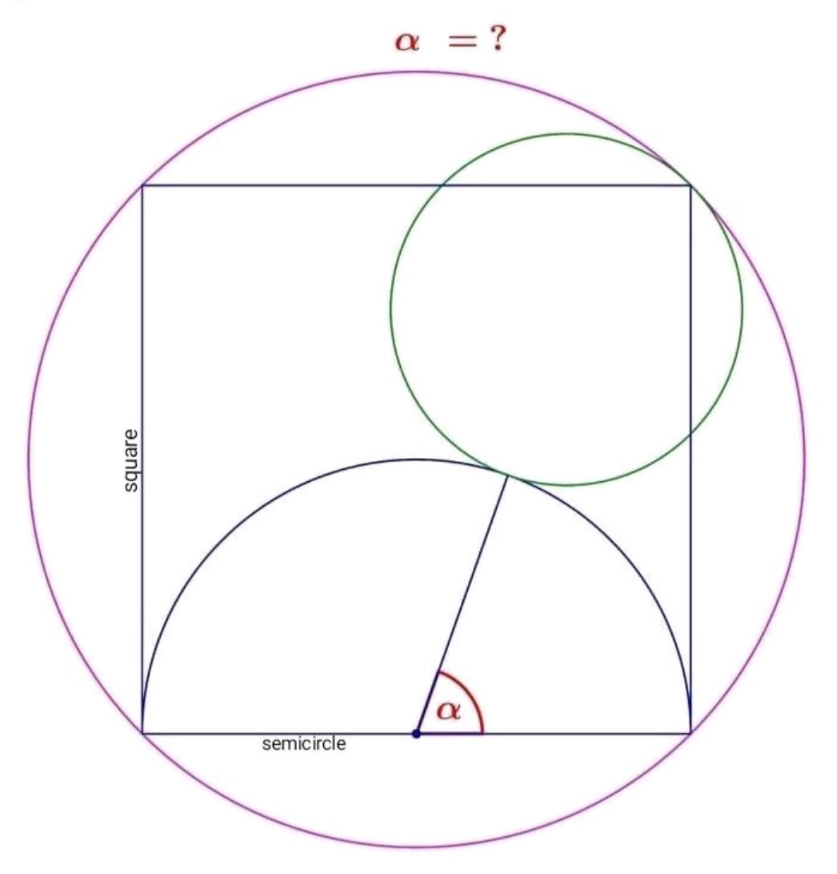
Question Number 193027 by Mingma last updated on 02/Jun/23
Answered by BaliramKumar last updated on 02/Jun/23

$$\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\sqrt{\mathrm{2}}\right)\:? \\ $$
Answered by ajfour last updated on 02/Jun/23

$$\left(\mathrm{1}+{r}\right)\mathrm{cos}\:\alpha+\frac{{r}}{\:\sqrt{\mathrm{2}}}=\mathrm{1} \\ $$$$\left(\mathrm{1}+{r}\right)\mathrm{sin}\:\alpha+\frac{{r}}{\:\sqrt{\mathrm{2}}}=\mathrm{2} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{2}−\frac{{r}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{{r}}{\:\sqrt{\mathrm{2}}}} \\ $$$$\left(\mathrm{1}+{r}\right)^{\mathrm{2}} =\left(\mathrm{1}−\frac{{r}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\mathrm{2}−\frac{{r}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{r}+\mathrm{1}=\mathrm{5}−\frac{\mathrm{6}{r}}{\:\sqrt{\mathrm{2}}} \\ $$$${r}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}+\sqrt{\mathrm{2}}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}+\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}+\sqrt{\mathrm{2}}}}=\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$
Commented by Mingma last updated on 03/Jun/23
Perfect ��
