Question Number 193069 by Mingma last updated on 03/Jun/23
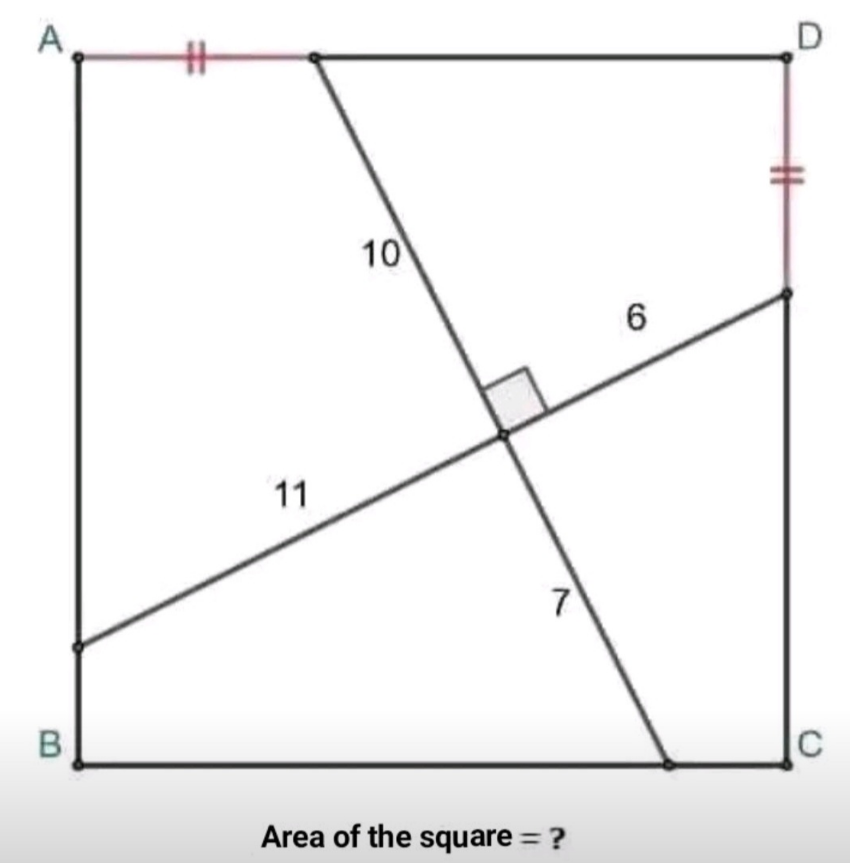
Answered by ajfour last updated on 03/Jun/23

Commented by ajfour last updated on 03/Jun/23

$${a}=\mathrm{17cos}\:\theta \\ $$$${p}\mathrm{sin}\:\theta+\mathrm{10sin}\:\theta+\mathrm{6cos}\:\theta={a}=\mathrm{17cos}\:\theta \\ $$$$\Rightarrow\:\:{p}+\mathrm{10}=\mathrm{11cot}\:\theta \\ $$$$\mathrm{cot}\:\theta=\frac{\mathrm{6}+{p}}{\mathrm{10}} \\ $$$$\Rightarrow\:\:\mathrm{10cos}\:\theta−\mathrm{6}+\mathrm{10}=\mathrm{11cot}\:\theta \\ $$$$\mathrm{10cos}\:\theta\mathrm{sin}\:\theta+\mathrm{4sin}\:\theta=\mathrm{11cos}\:\theta \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{10}{t}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{121}{t}^{\mathrm{2}} \\ $$$${t}=\mathrm{cos}\:\theta\approx\mathrm{0}.\mathrm{76483} \\ $$$${a}^{\mathrm{2}} =\mathrm{289}{t}^{\mathrm{2}} \approx\mathrm{169}.\mathrm{05}\:\:{sq}\:{units} \\ $$
Commented by MM42 last updated on 04/Jun/23

$${it}\:{was}\:{a}\:{beautiful}\:{solution}. \\ $$$${p}+\mathrm{10}=\mathrm{11}{cot}\theta \\ $$$${p}+\mathrm{6}=\mathrm{10}{cot}\theta \\ $$$$\Rightarrow{cot}\theta=\mathrm{4}\Rightarrow{cos}\theta=\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\Rightarrow{a}=\frac{\mathrm{20}}{\:\sqrt{\mathrm{17}}}\:\Rightarrow{s}=\frac{\mathrm{400}}{\mathrm{17}} \\ $$$$ \\ $$
