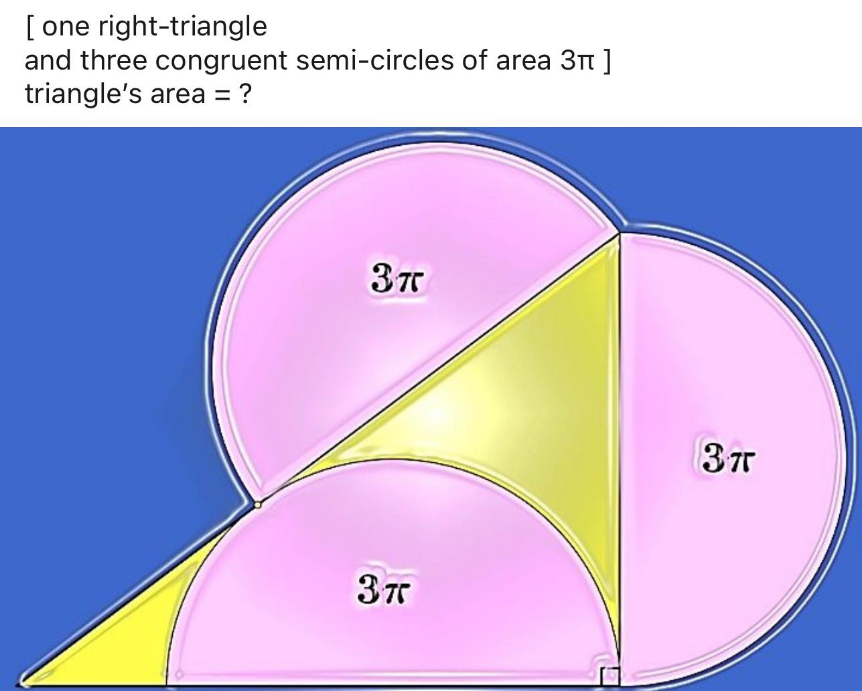
Question Number 193093 by Mingma last updated on 04/Jun/23
Answered by Subhi last updated on 04/Jun/23
![(1/2).π.r^2 = 3π r = (√6) AB = AD = BE = 2(√6) (CD)^2 = CE.BC=CE.(CE+2(√6)) (CD)^2 =(CE)^2 +2(√6).CE →(1) or {(CD)^2 +6=(CE+(√6))^2 =(CE)^2 +2(√6).CE+6} ((CD)/(sin(90−x)))=((√6)/(sin(x))) (sin law) ((sin(x))/(cos(x)))=((√6)/(CD)) ⇛ tan(x)=((√6)/(CD)) (i) in the Δ ABC ((2(√6))/(sin(x)))=((2(√6)+CE)/(sin(90−x))) tan(x) = ((2(√6))/(2(√6)+CE)) (ii) ((2(√6))/(2(√6)+CE))=((√6)/(CD)) CD = (√6)+((CE)/2) → (2) substitute in (1) 6+(√6).CE+(((CE)^2 )/4)=(CE)^2 +2(√6).CE (3/4)(CE)^2 +(√6).CE−6 = 0 CE = ((2(√6))/3) , CD = ((4(√6))/3) [ΔABC] = (1/2)×2(√6)×(2(√6)+((2(√6))/3))=16 the shaded area = 16−3π](https://www.tinkutara.com/question/Q193095.png)
$$\frac{\mathrm{1}}{\mathrm{2}}.\pi.{r}^{\mathrm{2}} \:=\:\mathrm{3}\pi \\ $$$${r}\:=\:\sqrt{\mathrm{6}} \\ $$$${AB}\:=\:{AD}\:=\:{BE}\:=\:\:\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\left({CD}\right)^{\mathrm{2}} \:=\:{CE}.{BC}={CE}.\left({CE}+\mathrm{2}\sqrt{\mathrm{6}}\right) \\ $$$$\left({CD}\right)^{\mathrm{2}} =\left({CE}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{6}}.{CE}\:\:\rightarrow\left(\mathrm{1}\right) \\ $$$${or} \\ $$$$\left\{\left({CD}\right)^{\mathrm{2}} +\mathrm{6}=\left({CE}+\sqrt{\mathrm{6}}\right)^{\mathrm{2}} =\left({CE}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{6}}.{CE}+\mathrm{6}\right\} \\ $$$$\frac{{CD}}{{sin}\left(\mathrm{90}−{x}\right)}=\frac{\sqrt{\mathrm{6}}}{{sin}\left({x}\right)}\:\:\:\:\:\left({sin}\:{law}\right) \\ $$$$\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)}=\frac{\sqrt{\mathrm{6}}}{{CD}}\:\:\Rrightarrow\:{tan}\left({x}\right)=\frac{\sqrt{\mathrm{6}}}{{CD}}\:\:\left({i}\right) \\ $$$${in}\:{the}\:\Delta\:{ABC} \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{6}}}{{sin}\left({x}\right)}=\frac{\mathrm{2}\sqrt{\mathrm{6}}+{CE}}{{sin}\left(\mathrm{90}−{x}\right)} \\ $$$${tan}\left({x}\right)\:=\:\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}\sqrt{\mathrm{6}}+{CE}}\:\:\:\left({ii}\right) \\ $$$$\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{2}\sqrt{\mathrm{6}}+{CE}}=\frac{\sqrt{\mathrm{6}}}{{CD}} \\ $$$${CD}\:=\:\sqrt{\mathrm{6}}+\frac{{CE}}{\mathrm{2}}\:\:\rightarrow\:\left(\mathrm{2}\right) \\ $$$${substitute}\:{in}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{6}+\sqrt{\mathrm{6}}.{CE}+\frac{\left({CE}\right)^{\mathrm{2}} }{\mathrm{4}}=\left({CE}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{6}}.{CE} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\left({CE}\right)^{\mathrm{2}} +\sqrt{\mathrm{6}}.{CE}−\mathrm{6}\:=\:\mathrm{0} \\ $$$${CE}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\:\:\:\:\:,\:\:{CD}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\left[\Delta{ABC}\right]\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{6}}×\left(\mathrm{2}\sqrt{\mathrm{6}}+\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)=\mathrm{16} \\ $$$${the}\:{shaded}\:{area}\:=\:\mathrm{16}−\mathrm{3}\pi \\ $$
Commented by Subhi last updated on 04/Jun/23

$${You}\:{can}\:{also}\:{use}\:{the}\:{similarity} \\ $$$$\Delta{DCO}\:{is}\:{similar}\:{to}\:\Delta{BCA} \\ $$$$\frac{{DC}}{{CE}+\mathrm{2}\sqrt{\mathrm{6}}}=\frac{{DO}}{{BA}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}\sqrt{\mathrm{6}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{DC}\:=\:{CE}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$
Commented by Subhi last updated on 04/Jun/23

Commented by Mingma last updated on 04/Jun/23
Perfect ��
