Question Number 19557 by ajfour last updated on 12/Aug/17
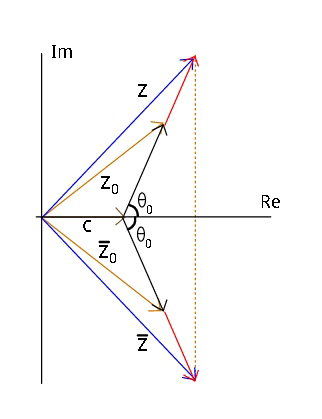
Commented by ajfour last updated on 12/Aug/17
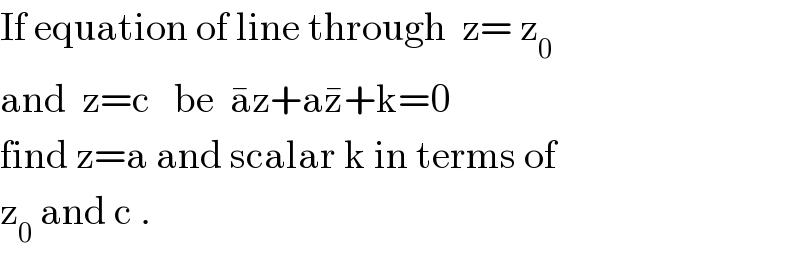
$$\mathrm{If}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{through}\:\:\mathrm{z}=\:\mathrm{z}_{\mathrm{0}} \\ $$$$\mathrm{and}\:\:\mathrm{z}=\mathrm{c}\:\:\:\mathrm{be}\:\:\bar {\mathrm{a}z}+\mathrm{a}\bar {\mathrm{z}}+\mathrm{k}=\mathrm{0} \\ $$$$\mathrm{find}\:\mathrm{z}=\mathrm{a}\:\mathrm{and}\:\mathrm{scalar}\:\mathrm{k}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{z}_{\mathrm{0}} \:\mathrm{and}\:\mathrm{c}\:. \\ $$
Commented by Tinkutara last updated on 12/Aug/17

$$\mathrm{Yes}! \\ $$
Commented by ajfour last updated on 12/Aug/17
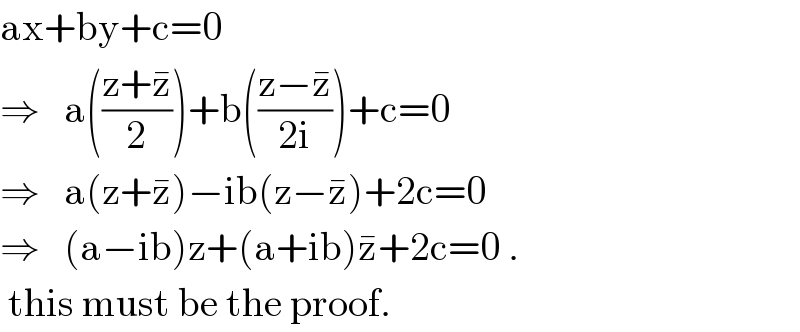
$$\mathrm{ax}+\mathrm{by}+\mathrm{c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{a}\left(\frac{\mathrm{z}+\bar {\mathrm{z}}}{\mathrm{2}}\right)+\mathrm{b}\left(\frac{\mathrm{z}−\bar {\mathrm{z}}}{\mathrm{2i}}\right)+\mathrm{c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{a}\left(\mathrm{z}+\bar {\mathrm{z}}\right)−\mathrm{ib}\left(\mathrm{z}−\bar {\mathrm{z}}\right)+\mathrm{2c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{a}−\mathrm{ib}\right)\mathrm{z}+\left(\mathrm{a}+\mathrm{ib}\right)\bar {\mathrm{z}}+\mathrm{2c}=\mathrm{0}\:. \\ $$$$\:\mathrm{this}\:\mathrm{must}\:\mathrm{be}\:\mathrm{the}\:\mathrm{proof}. \\ $$
Answered by ajfour last updated on 13/Aug/17
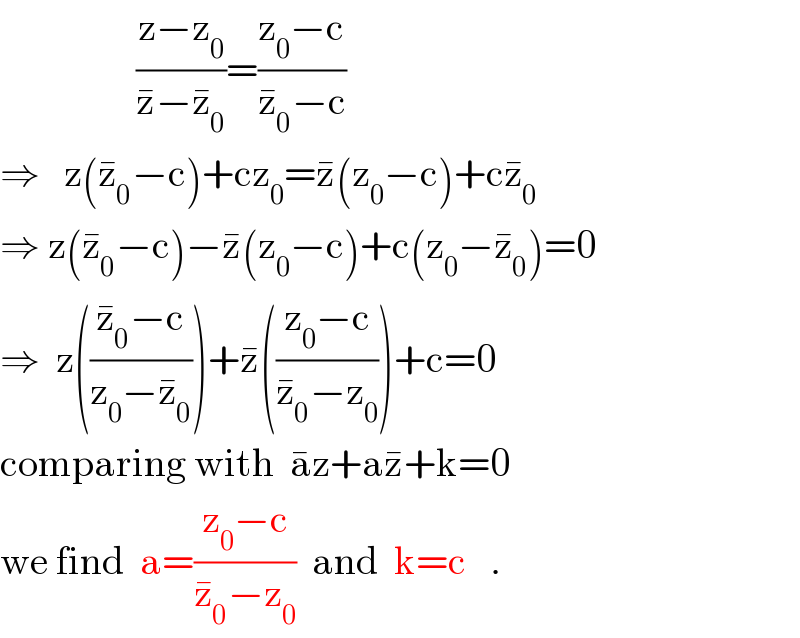
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{z}−\mathrm{z}_{\mathrm{0}} }{\bar {\mathrm{z}}−\bar {\mathrm{z}}_{\mathrm{0}} }=\frac{\mathrm{z}_{\mathrm{0}} −\mathrm{c}}{\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{c}} \\ $$$$\Rightarrow\:\:\:\mathrm{z}\left(\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{c}\right)+\mathrm{cz}_{\mathrm{0}} =\bar {\mathrm{z}}\left(\mathrm{z}_{\mathrm{0}} −\mathrm{c}\right)+\mathrm{c}\bar {\mathrm{z}}_{\mathrm{0}} \\ $$$$\Rightarrow\:\mathrm{z}\left(\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{c}\right)−\bar {\mathrm{z}}\left(\mathrm{z}_{\mathrm{0}} −\mathrm{c}\right)+\mathrm{c}\left(\mathrm{z}_{\mathrm{0}} −\bar {\mathrm{z}}_{\mathrm{0}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{z}\left(\frac{\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{c}}{\mathrm{z}_{\mathrm{0}} −\bar {\mathrm{z}}_{\mathrm{0}} }\right)+\bar {\mathrm{z}}\left(\frac{\mathrm{z}_{\mathrm{0}} −\mathrm{c}}{\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{z}_{\mathrm{0}} }\right)+\mathrm{c}=\mathrm{0} \\ $$$$\mathrm{comparing}\:\mathrm{with}\:\:\bar {\mathrm{a}z}+\mathrm{a}\bar {\mathrm{z}}+\mathrm{k}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{find}\:\:\mathrm{a}=\frac{\mathrm{z}_{\mathrm{0}} −\mathrm{c}}{\bar {\mathrm{z}}_{\mathrm{0}} −\mathrm{z}_{\mathrm{0}} }\:\:\mathrm{and}\:\:\mathrm{k}=\mathrm{c}\:\:\:. \\ $$
