Menu Close

Question-19592

Tinku Tara 0 Comments
Pin




Question Number 19592 by ajfour last updated on 13/Aug/17
Commented by Tinkutara last updated on 13/Aug/17
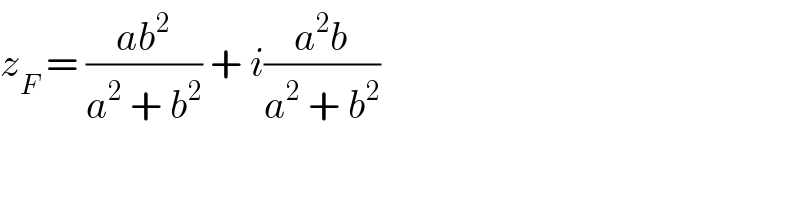
z_F = ((ab^2 )/(a^2 + b^2 )) + i((a^2 b)/(a^2 + b^2 ))
$${z}_{{F}} \:=\:\frac{{ab}^{\mathrm{2}} }{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} }\:+\:{i}\frac{{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 13/Aug/17
If we seek to find equation of line shown above, z=z_F +iλz_F and z^� =z_F ^� −iλz_F ^� so ((z−z_F )/(z^� −z_F ^� ))= −(z_F /z_F ^� ) ⇒ z_F ^� z−∣z_F ∣^2 = −z_F z^� +∣z_F ∣^2 ⇒ z_F ^� z+z_F z^� −2∣z_F ∣^2 =0 if equation of line be α^� z+αz^� +2c=0 then this means α=z_F and c=−∣z_F ∣^2 . complex slope =−(α/α^� ) =−(z_F /z_F ^� ) . =−(((b+ia)/(b−ia)))×(i/i) =((a−ib)/(a+ib)) .
$$\:\:\:\:\mathrm{If}\:\mathrm{we}\:\mathrm{seek}\:\mathrm{to}\:\mathrm{find}\:\mathrm{equation}\:\mathrm{of} \\ $$$$\mathrm{line}\:\mathrm{shown}\:\mathrm{above},\:\mathrm{z}=\mathrm{z}_{\mathrm{F}} +\mathrm{i}\lambda\mathrm{z}_{\mathrm{F}} \\ $$$$\:\:\:\:\:\mathrm{and}\:\:\:\:\bar {\mathrm{z}}=\bar {\mathrm{z}}_{\mathrm{F}} −\mathrm{i}\lambda\bar {\mathrm{z}}_{\mathrm{F}} \:\: \\ $$$$\mathrm{so}\:\frac{\mathrm{z}−\mathrm{z}_{\mathrm{F}} }{\bar {\mathrm{z}}−\bar {\mathrm{z}}_{\mathrm{F}} }=\:−\frac{\mathrm{z}_{\mathrm{F}} }{\bar {\mathrm{z}}_{\mathrm{F}} } \\ $$$$\Rightarrow\:\:\:\bar {\mathrm{z}}_{\mathrm{F}} \mathrm{z}−\mid\mathrm{z}_{\mathrm{F}} \mid^{\mathrm{2}} \:=\:−\mathrm{z}_{\mathrm{F}} \bar {\mathrm{z}}+\mid\mathrm{z}_{\mathrm{F}} \mid^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\bar {\mathrm{z}}_{\mathrm{F}} \mathrm{z}+\mathrm{z}_{\mathrm{F}} \bar {\mathrm{z}}−\mathrm{2}\mid\mathrm{z}_{\mathrm{F}} \mid^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{if}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{be} \\ $$$$\:\:\:\:\:\:\:\:\:\bar {\alpha}\mathrm{z}+\alpha\bar {\mathrm{z}}+\mathrm{2c}=\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{this}\:\mathrm{means}\:\:\alpha=\mathrm{z}_{\mathrm{F}} \:\mathrm{and}\:\mathrm{c}=−\mid\mathrm{z}_{\mathrm{F}} \mid^{\mathrm{2}} \:. \\ $$$$\mathrm{complex}\:\mathrm{slope}\:=−\frac{\alpha}{\bar {\alpha}}\:=−\frac{\mathrm{z}_{\mathrm{F}} }{\bar {\mathrm{z}}_{\mathrm{F}} }\:\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\left(\frac{\mathrm{b}+\mathrm{ia}}{\mathrm{b}−\mathrm{ia}}\right)×\frac{\mathrm{i}}{\mathrm{i}}\:=\frac{\mathrm{a}−\mathrm{ib}}{\mathrm{a}+\mathrm{ib}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *