Question Number 19604 by ajfour last updated on 13/Aug/17
Commented by ajfour last updated on 13/Aug/17
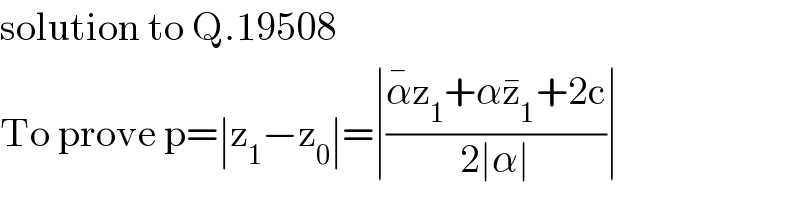
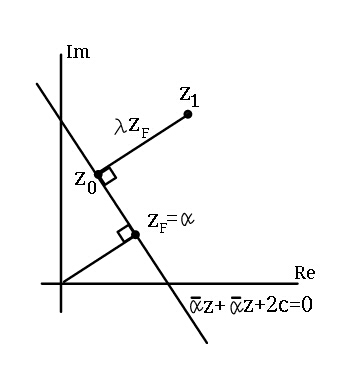
$$\mathrm{solution}\:\mathrm{to}\:\mathrm{Q}.\mathrm{19508} \\ $$$$\mathrm{To}\:\mathrm{prove}\:\mathrm{p}=\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{0}} \mid=\mid\frac{\bar {\alpha}\mathrm{z}_{\mathrm{1}} +\alpha\bar {\mathrm{z}}_{\mathrm{1}} +\mathrm{2c}}{\mathrm{2}\mid\alpha\mid}\mid \\ $$
Answered by ajfour last updated on 13/Aug/17
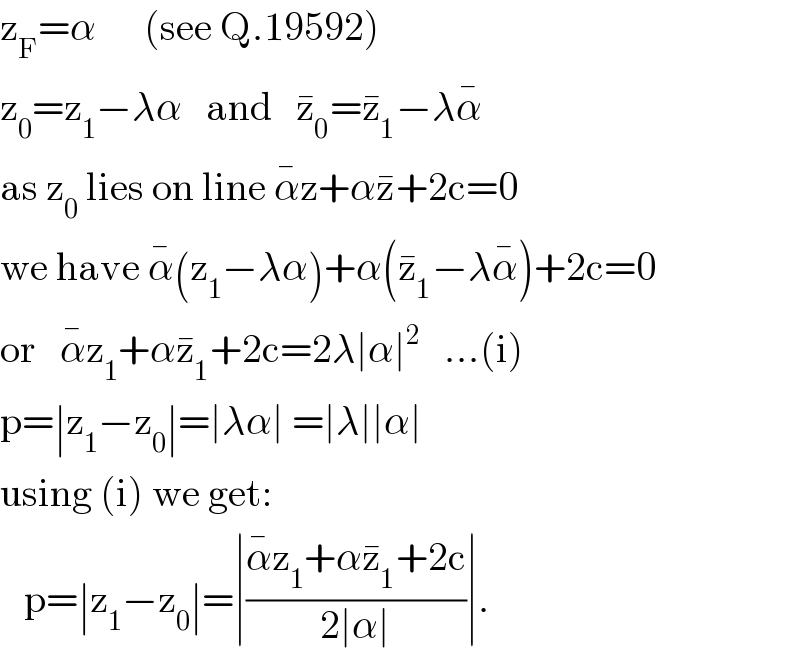
$$\mathrm{z}_{\mathrm{F}} =\alpha\:\:\:\:\:\:\left(\mathrm{see}\:\mathrm{Q}.\mathrm{19592}\right) \\ $$$$\mathrm{z}_{\mathrm{0}} =\mathrm{z}_{\mathrm{1}} −\lambda\alpha\:\:\:\mathrm{and}\:\:\:\bar {\mathrm{z}}_{\mathrm{0}} =\bar {\mathrm{z}}_{\mathrm{1}} −\lambda\bar {\alpha} \\ $$$$\mathrm{as}\:\mathrm{z}_{\mathrm{0}} \:\mathrm{lies}\:\mathrm{on}\:\mathrm{line}\:\bar {\alpha}\mathrm{z}+\alpha\bar {\mathrm{z}}+\mathrm{2c}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{have}\:\bar {\alpha}\left(\mathrm{z}_{\mathrm{1}} −\lambda\alpha\right)+\alpha\left(\bar {\mathrm{z}}_{\mathrm{1}} −\lambda\bar {\alpha}\right)+\mathrm{2c}=\mathrm{0} \\ $$$$\mathrm{or}\:\:\:\bar {\alpha}\mathrm{z}_{\mathrm{1}} +\alpha\bar {\mathrm{z}}_{\mathrm{1}} +\mathrm{2c}=\mathrm{2}\lambda\mid\alpha\mid^{\mathrm{2}} \:\:\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{p}=\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{0}} \mid=\mid\lambda\alpha\mid\:=\mid\lambda\mid\mid\alpha\mid \\ $$$$\mathrm{using}\:\left(\mathrm{i}\right)\:\mathrm{we}\:\mathrm{get}: \\ $$$$\:\:\:\mathrm{p}=\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{0}} \mid=\mid\frac{\bar {\alpha}\mathrm{z}_{\mathrm{1}} +\alpha\bar {\mathrm{z}}_{\mathrm{1}} +\mathrm{2c}}{\mathrm{2}\mid\alpha\mid}\mid. \\ $$
Commented by Tinkutara last updated on 13/Aug/17
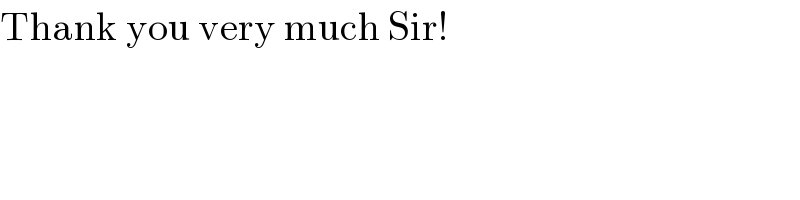
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
