Question-19736

Question Number 19736 by ajfour last updated on 15/Aug/17

Commented by ajfour last updated on 15/Aug/17

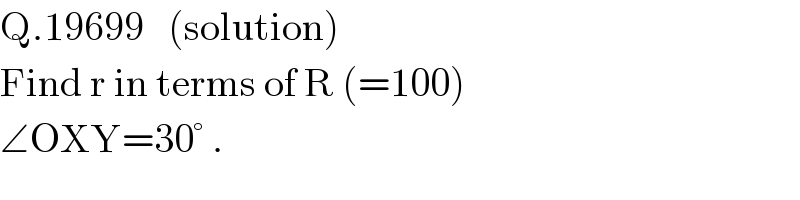
Q.19699 (solution) Find r in terms of R (=100) ∠OXY=30° .

$$\mathrm{Q}.\mathrm{19699}\:\:\:\left(\mathrm{solution}\right) \\ $$$$\mathrm{Find}\:\mathrm{r}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{R}\:\left(=\mathrm{100}\right) \\ $$$$\angle\mathrm{OXY}=\mathrm{30}°\:. \\ $$

Answered by ajfour last updated on 15/Aug/17

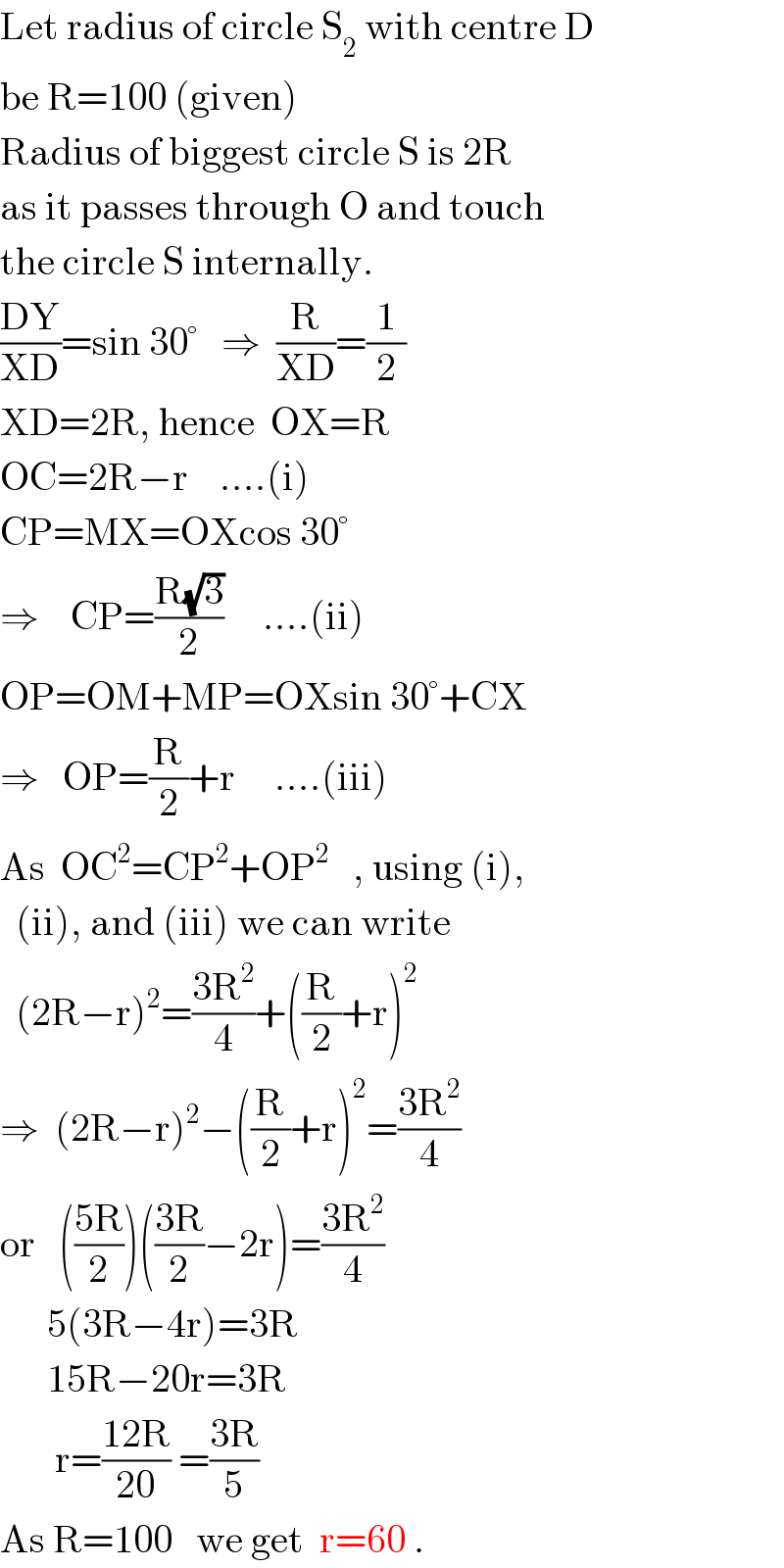
Let radius of circle S_2 with centre D be R=100 (given) Radius of biggest circle S is 2R as it passes through O and touch the circle S internally. ((DY)/(XD))=sin 30° ⇒ (R/(XD))=(1/2) XD=2R, hence OX=R OC=2R−r ....(i) CP=MX=OXcos 30° ⇒ CP=((R(√3))/2) ....(ii) OP=OM+MP=OXsin 30°+CX ⇒ OP=(R/2)+r ....(iii) As OC^2 =CP^2 +OP^2 , using (i), (ii), and (iii) we can write (2R−r)^2 =((3R^2 )/4)+((R/2)+r)^2 ⇒ (2R−r)^2 −((R/2)+r)^2 =((3R^2 )/4) or (((5R)/2))(((3R)/2)−2r)=((3R^2 )/4) 5(3R−4r)=3R 15R−20r=3R r=((12R)/(20)) =((3R)/5) As R=100 we get r=60 .

$$\mathrm{Let}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{S}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{centre}\:\mathrm{D} \\ $$$$\mathrm{be}\:\mathrm{R}=\mathrm{100}\:\left(\mathrm{given}\right) \\ $$$$\mathrm{Radius}\:\mathrm{of}\:\mathrm{biggest}\:\mathrm{circle}\:\mathrm{S}\:\mathrm{is}\:\mathrm{2R} \\ $$$$\mathrm{as}\:\mathrm{it}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{O}\:\mathrm{and}\:\mathrm{touch} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{S}\:\mathrm{internally}. \\ $$$$\frac{\mathrm{DY}}{\mathrm{XD}}=\mathrm{sin}\:\mathrm{30}°\:\:\:\Rightarrow\:\:\frac{\mathrm{R}}{\mathrm{XD}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{XD}=\mathrm{2R},\:\mathrm{hence}\:\:\mathrm{OX}=\mathrm{R} \\ $$$$\mathrm{OC}=\mathrm{2R}−\mathrm{r}\:\:\:\:….\left(\mathrm{i}\right) \\ $$$$\mathrm{CP}=\mathrm{MX}=\mathrm{OXcos}\:\mathrm{30}° \\ $$$$\Rightarrow\:\:\:\:\mathrm{CP}=\frac{\mathrm{R}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:….\left(\mathrm{ii}\right) \\ $$$$\mathrm{OP}=\mathrm{OM}+\mathrm{MP}=\mathrm{OXsin}\:\mathrm{30}°+\mathrm{CX} \\ $$$$\Rightarrow\:\:\:\mathrm{OP}=\frac{\mathrm{R}}{\mathrm{2}}+\mathrm{r}\:\:\:\:\:….\left(\mathrm{iii}\right) \\ $$$$\mathrm{As}\:\:\mathrm{OC}^{\mathrm{2}} =\mathrm{CP}^{\mathrm{2}} +\mathrm{OP}^{\mathrm{2}} \:\:\:,\:\mathrm{using}\:\left(\mathrm{i}\right), \\ $$$$\:\:\left(\mathrm{ii}\right),\:\mathrm{and}\:\left(\mathrm{iii}\right)\:\mathrm{we}\:\mathrm{can}\:\mathrm{write} \\ $$$$\:\:\left(\mathrm{2R}−\mathrm{r}\right)^{\mathrm{2}} =\frac{\mathrm{3R}^{\mathrm{2}} }{\mathrm{4}}+\left(\frac{\mathrm{R}}{\mathrm{2}}+\mathrm{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\mathrm{2R}−\mathrm{r}\right)^{\mathrm{2}} −\left(\frac{\mathrm{R}}{\mathrm{2}}+\mathrm{r}\right)^{\mathrm{2}} =\frac{\mathrm{3R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{or}\:\:\:\left(\frac{\mathrm{5R}}{\mathrm{2}}\right)\left(\frac{\mathrm{3R}}{\mathrm{2}}−\mathrm{2r}\right)=\frac{\mathrm{3R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\mathrm{5}\left(\mathrm{3R}−\mathrm{4r}\right)=\mathrm{3R} \\ $$$$\:\:\:\:\:\:\mathrm{15R}−\mathrm{20r}=\mathrm{3R} \\ $$$$\:\:\:\:\:\:\:\mathrm{r}=\frac{\mathrm{12R}}{\mathrm{20}}\:=\frac{\mathrm{3R}}{\mathrm{5}}\:\:\: \\ $$$$\mathrm{As}\:\mathrm{R}=\mathrm{100}\:\:\:\mathrm{we}\:\mathrm{get}\:\:\mathrm{r}=\mathrm{60}\:. \\ $$

Commented by Tinkutara last updated on 15/Aug/17

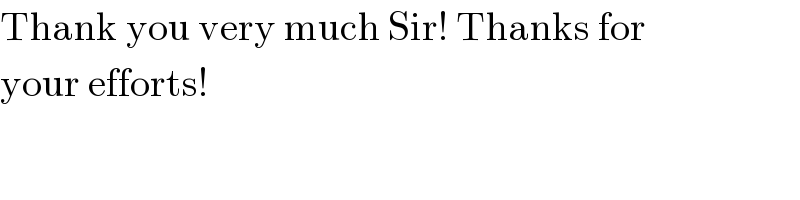
Thank you very much Sir! Thanks for your efforts!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}!\:\mathrm{Thanks}\:\mathrm{for} \\ $$$$\mathrm{your}\:\mathrm{efforts}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply