Question Number 19758 by ajfour last updated on 15/Aug/17
Commented by ajfour last updated on 15/Aug/17

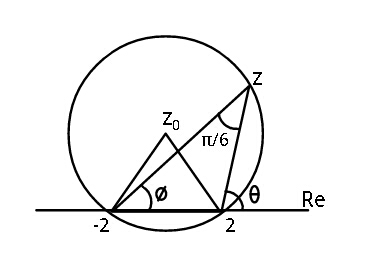
$$\mathrm{In}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{Q}.\mathrm{19741} \\ $$
Answered by ajfour last updated on 15/Aug/17
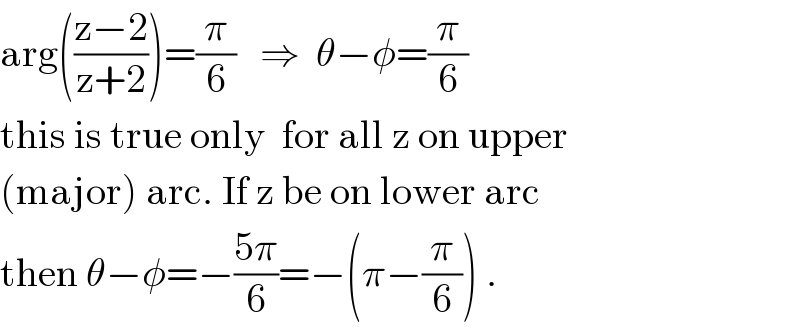
$$\mathrm{arg}\left(\frac{\mathrm{z}−\mathrm{2}}{\mathrm{z}+\mathrm{2}}\right)=\frac{\pi}{\mathrm{6}}\:\:\:\Rightarrow\:\:\theta−\phi=\frac{\pi}{\mathrm{6}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{true}\:\mathrm{only}\:\:\mathrm{for}\:\mathrm{all}\:\mathrm{z}\:\mathrm{on}\:\mathrm{upper} \\ $$$$\left(\mathrm{major}\right)\:\mathrm{arc}.\:\mathrm{If}\:\mathrm{z}\:\mathrm{be}\:\mathrm{on}\:\mathrm{lower}\:\mathrm{arc} \\ $$$$\mathrm{then}\:\theta−\phi=−\frac{\mathrm{5}\pi}{\mathrm{6}}=−\left(\pi−\frac{\pi}{\mathrm{6}}\right)\:. \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
