Question-19796

Question Number 19796 by ajfour last updated on 15/Aug/17

Commented by ajfour last updated on 15/Aug/17

$$\mathrm{Q}.\mathrm{19794}\:\:\:\left(\mathrm{solution}\right) \\ $$

Answered by ajfour last updated on 15/Aug/17

let presently AB=2 let area of △ABC=4Δ area of △AXZ = Δ Area of △XYZ=(tan^2 θ)Δ (because △XYZ ∼ △AXZ) Area BXYC= Area CWXZ+ Area △BXW−Area(△AXZ) =2Δ+Δ−(tan^2 θ)Δ ((Area BXYC)/(Area △ABC))=((3Δ−(tan^2 θ)Δ)/(4Δ))=((13)/(18)) ⇒ 3−tan^2 θ=((26)/9) So tan^2 θ=(1/9) Now tan θ=(1/3)=((BC)/(AC)) ⇒ AC=3(BC) =3×12 =36 .

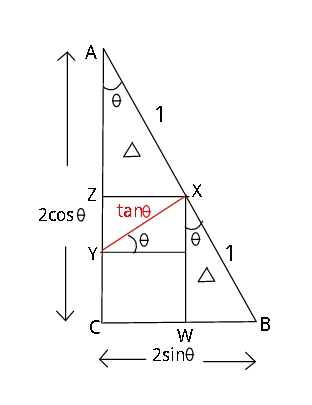
$$\mathrm{let}\:\mathrm{presently}\:\mathrm{AB}=\mathrm{2} \\ $$$$\mathrm{let}\:\mathrm{area}\:\mathrm{of}\:\bigtriangleup\mathrm{ABC}=\mathrm{4}\Delta \\ $$$$\mathrm{area}\:\mathrm{of}\:\bigtriangleup\mathrm{AXZ}\:=\:\Delta \\ $$$$\mathrm{Area}\:\mathrm{of}\:\bigtriangleup\mathrm{XYZ}=\left(\mathrm{tan}\:^{\mathrm{2}} \theta\right)\Delta \\ $$$$\:\:\:\left(\mathrm{because}\:\bigtriangleup\mathrm{XYZ}\:\sim\:\bigtriangleup\mathrm{AXZ}\right) \\ $$$$\mathrm{Area}\:\mathrm{BXYC}=\:\mathrm{Area}\:\mathrm{CWXZ}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{Area}\:\bigtriangleup\mathrm{BXW}−\mathrm{Area}\left(\bigtriangleup\mathrm{AXZ}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\Delta+\Delta−\left(\mathrm{tan}\:^{\mathrm{2}} \theta\right)\Delta \\ $$$$\frac{\mathrm{Area}\:\mathrm{BXYC}}{\mathrm{Area}\:\bigtriangleup\mathrm{ABC}}=\frac{\mathrm{3}\Delta−\left(\mathrm{tan}\:^{\mathrm{2}} \theta\right)\Delta}{\mathrm{4}\Delta}=\frac{\mathrm{13}}{\mathrm{18}} \\ $$$$\Rightarrow\:\:\:\mathrm{3}−\mathrm{tan}\:^{\mathrm{2}} \theta=\frac{\mathrm{26}}{\mathrm{9}}\:\:\: \\ $$$$\mathrm{So}\:\:\:\:\mathrm{tan}\:^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{Now}\:\:\:\:\:\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{BC}}{\mathrm{AC}}\: \\ $$$$\Rightarrow\:\:\:\mathrm{AC}=\mathrm{3}\left(\mathrm{BC}\right)\:=\mathrm{3}×\mathrm{12}\:=\mathrm{36}\:. \\ $$

Commented by Tinkutara last updated on 15/Aug/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply