Question Number 19875 by ajfour last updated on 16/Aug/17
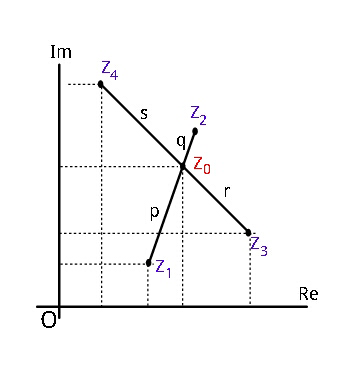
Commented by ajfour last updated on 17/Aug/17
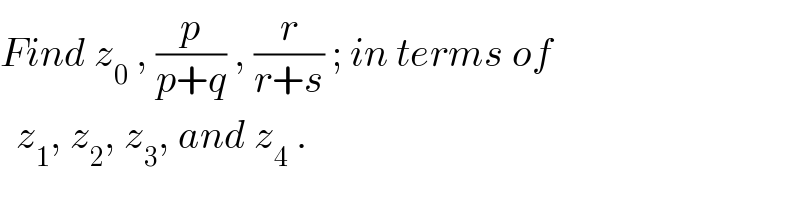
$${Find}\:{z}_{\mathrm{0}} \:,\:\frac{{p}}{{p}+{q}}\:,\:\frac{{r}}{{r}+{s}}\:;\:{in}\:{terms}\:{of} \\ $$$$\:\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} ,\:{z}_{\mathrm{3}} ,\:{and}\:{z}_{\mathrm{4}} \:. \\ $$
Answered by ajfour last updated on 17/Aug/17
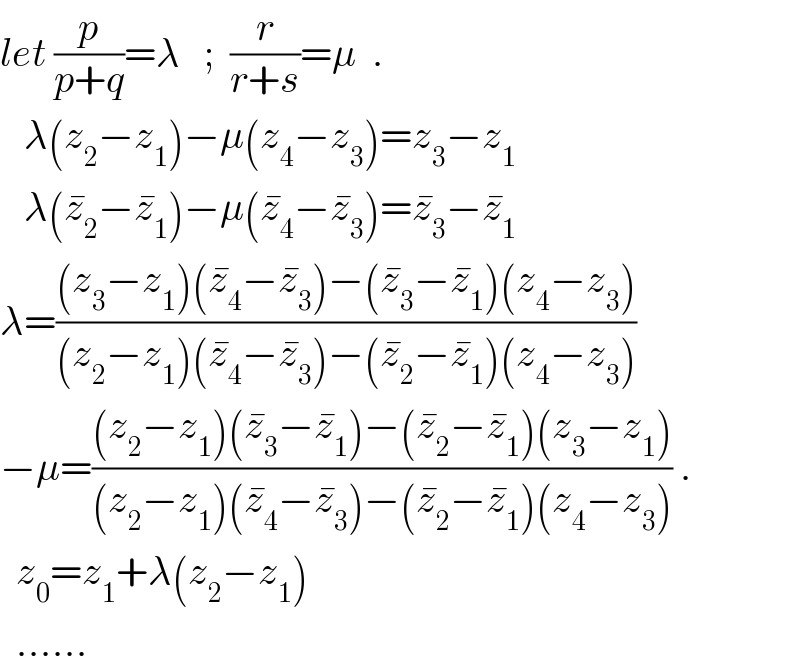
$${let}\:\frac{{p}}{{p}+{q}}=\lambda\:\:\:;\:\:\frac{{r}}{{r}+{s}}=\mu\:\:. \\ $$$$\:\:\:\lambda\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)−\mu\left({z}_{\mathrm{4}} −{z}_{\mathrm{3}} \right)={z}_{\mathrm{3}} −{z}_{\mathrm{1}} \\ $$$$\:\:\:\lambda\left(\bar {{z}}_{\mathrm{2}} −\bar {{z}}_{\mathrm{1}} \right)−\mu\left(\bar {{z}}_{\mathrm{4}} −\bar {{z}}_{\mathrm{3}} \right)=\bar {{z}}_{\mathrm{3}} −\bar {{z}}_{\mathrm{1}} \:\: \\ $$$$\lambda=\frac{\left({z}_{\mathrm{3}} −{z}_{\mathrm{1}} \right)\left(\bar {{z}}_{\mathrm{4}} −\bar {{z}}_{\mathrm{3}} \right)−\left(\bar {{z}}_{\mathrm{3}} −\bar {{z}}_{\mathrm{1}} \right)\left({z}_{\mathrm{4}} −{z}_{\mathrm{3}} \right)}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)\left(\bar {{z}}_{\mathrm{4}} −\bar {{z}}_{\mathrm{3}} \right)−\left(\bar {{z}}_{\mathrm{2}} −\bar {{z}}_{\mathrm{1}} \right)\left({z}_{\mathrm{4}} −{z}_{\mathrm{3}} \right)} \\ $$$$−\mu=\frac{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)\left(\bar {{z}}_{\mathrm{3}} −\bar {{z}}_{\mathrm{1}} \right)−\left(\bar {{z}}_{\mathrm{2}} −\bar {{z}}_{\mathrm{1}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{1}} \right)}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)\left(\bar {{z}}_{\mathrm{4}} −\bar {{z}}_{\mathrm{3}} \right)−\left(\bar {{z}}_{\mathrm{2}} −\bar {{z}}_{\mathrm{1}} \right)\left({z}_{\mathrm{4}} −{z}_{\mathrm{3}} \right)}\:. \\ $$$$\:\:{z}_{\mathrm{0}} ={z}_{\mathrm{1}} +\lambda\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right) \\ $$$$\:\:…… \\ $$
