Question Number 20031 by mondodotto@gmail.com last updated on 20/Aug/17
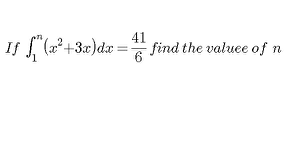
Answered by Tinkutara last updated on 20/Aug/17
![∫_1 ^n (x^2 + 3x)dx = [(x^3 /3) + ((3x^2 )/2)]_1 ^n = (n^3 /3) + ((3n^2 )/2) − (1/3) − (3/2) = ((41)/6) (n^3 /3) + ((3n^2 )/2) = ((26)/3) 2n^3 + 9n^2 − 52 = 0 (n − 2)(2n^2 + 13x + 26) = 0 ⇒ n = 2](https://www.tinkutara.com/question/Q20032.png)
$$\underset{\mathrm{1}} {\overset{{n}} {\int}}\left({x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\right){dx}\:=\:\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}} ^{{n}} \\ $$$$=\:\frac{{n}^{\mathrm{3}} }{\mathrm{3}}\:+\:\frac{\mathrm{3}{n}^{\mathrm{2}} }{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{41}}{\mathrm{6}} \\ $$$$\frac{{n}^{\mathrm{3}} }{\mathrm{3}}\:+\:\frac{\mathrm{3}{n}^{\mathrm{2}} }{\mathrm{2}}\:=\:\frac{\mathrm{26}}{\mathrm{3}} \\ $$$$\mathrm{2}{n}^{\mathrm{3}} \:+\:\mathrm{9}{n}^{\mathrm{2}} \:−\:\mathrm{52}\:=\:\mathrm{0} \\ $$$$\left({n}\:−\:\mathrm{2}\right)\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{13}{x}\:+\:\mathrm{26}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{n}\:=\:\mathrm{2} \\ $$
Commented by mondodotto@gmail.com last updated on 20/Aug/17

$$\mathrm{thanks}\: \\ $$
