Question Number 20036 by mondodotto@gmail.com last updated on 20/Aug/17
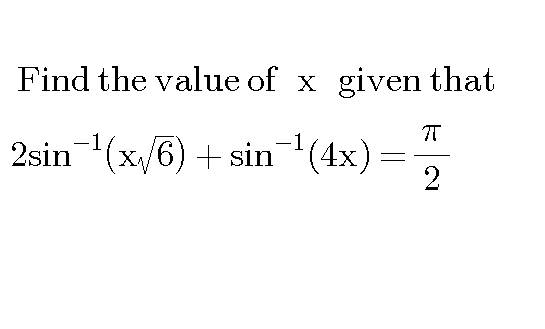
Answered by sma3l2996 last updated on 21/Aug/17
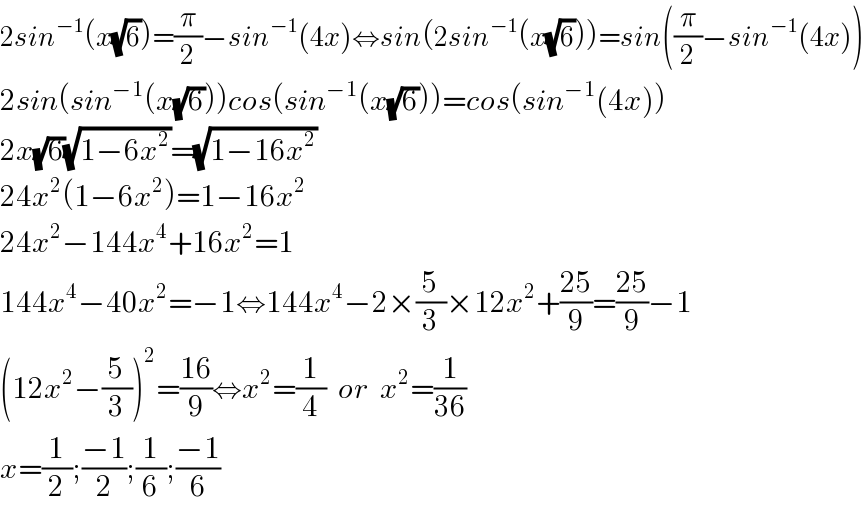
$$\mathrm{2}{sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{6}}\right)=\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left(\mathrm{4}{x}\right)\Leftrightarrow{sin}\left(\mathrm{2}{sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{6}}\right)\right)={sin}\left(\frac{\pi}{\mathrm{2}}−{sin}^{−\mathrm{1}} \left(\mathrm{4}{x}\right)\right) \\ $$$$\mathrm{2}{sin}\left({sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{6}}\right)\right){cos}\left({sin}^{−\mathrm{1}} \left({x}\sqrt{\mathrm{6}}\right)\right)={cos}\left({sin}^{−\mathrm{1}} \left(\mathrm{4}{x}\right)\right) \\ $$$$\mathrm{2}{x}\sqrt{\mathrm{6}}\sqrt{\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} }=\sqrt{\mathrm{1}−\mathrm{16}{x}^{\mathrm{2}} } \\ $$$$\mathrm{24}{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{6}{x}^{\mathrm{2}} \right)=\mathrm{1}−\mathrm{16}{x}^{\mathrm{2}} \\ $$$$\mathrm{24}{x}^{\mathrm{2}} −\mathrm{144}{x}^{\mathrm{4}} +\mathrm{16}{x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{144}{x}^{\mathrm{4}} −\mathrm{40}{x}^{\mathrm{2}} =−\mathrm{1}\Leftrightarrow\mathrm{144}{x}^{\mathrm{4}} −\mathrm{2}×\frac{\mathrm{5}}{\mathrm{3}}×\mathrm{12}{x}^{\mathrm{2}} +\frac{\mathrm{25}}{\mathrm{9}}=\frac{\mathrm{25}}{\mathrm{9}}−\mathrm{1} \\ $$$$\left(\mathrm{12}{x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{16}}{\mathrm{9}}\Leftrightarrow{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\:\:{or}\:\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{36}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}};\frac{−\mathrm{1}}{\mathrm{2}};\frac{\mathrm{1}}{\mathrm{6}};\frac{−\mathrm{1}}{\mathrm{6}} \\ $$
