Question Number 20044 by mondodotto@gmail.com last updated on 20/Aug/17

Answered by $@ty@m last updated on 20/Aug/17
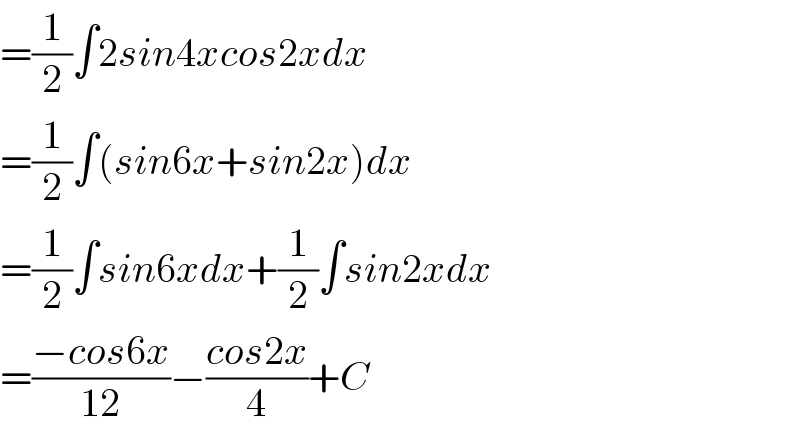
$$=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{2}{sin}\mathrm{4}{xcos}\mathrm{2}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left({sin}\mathrm{6}{x}+{sin}\mathrm{2}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{sin}\mathrm{6}{xdx}+\frac{\mathrm{1}}{\mathrm{2}}\int{sin}\mathrm{2}{xdx} \\ $$$$=\frac{−{cos}\mathrm{6}{x}}{\mathrm{12}}−\frac{{cos}\mathrm{2}{x}}{\mathrm{4}}+{C} \\ $$
Answered by mrW1 last updated on 21/Aug/17
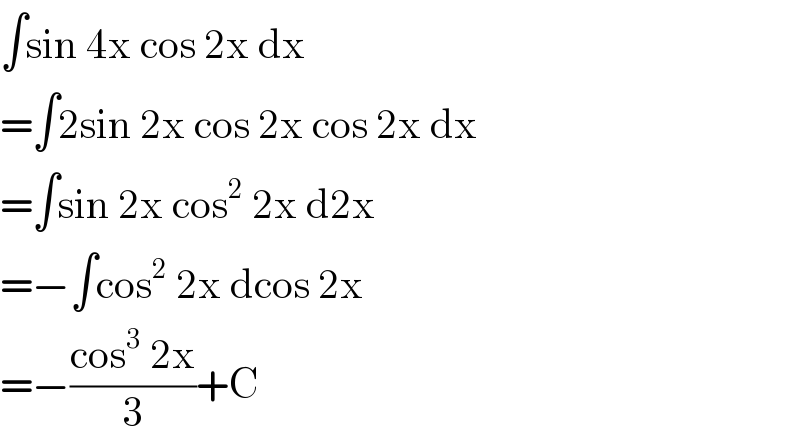
$$\int\mathrm{sin}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{dx} \\ $$$$=\int\mathrm{2sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{dx} \\ $$$$=\int\mathrm{sin}\:\mathrm{2x}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{2x}\:\mathrm{d2x} \\ $$$$=−\int\mathrm{cos}^{\mathrm{2}} \:\mathrm{2x}\:\mathrm{dcos}\:\mathrm{2x} \\ $$$$=−\frac{\mathrm{cos}^{\mathrm{3}} \:\mathrm{2x}}{\mathrm{3}}+\mathrm{C} \\ $$
