Question Number 20488 by xing last updated on 27/Aug/17

Commented by ajfour last updated on 27/Aug/17
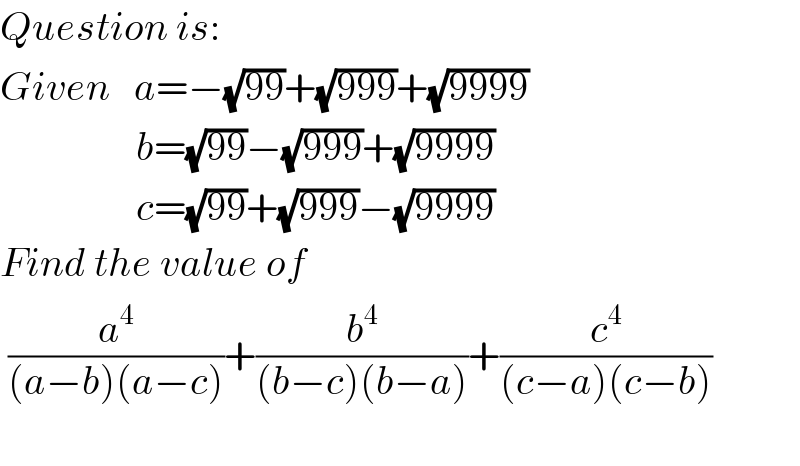
$${Question}\:{is}: \\ $$$${Given}\:\:\:{a}=−\sqrt{\mathrm{99}}+\sqrt{\mathrm{999}}+\sqrt{\mathrm{9999}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}=\sqrt{\mathrm{99}}−\sqrt{\mathrm{999}}+\sqrt{\mathrm{9999}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}=\sqrt{\mathrm{99}}+\sqrt{\mathrm{999}}−\sqrt{\mathrm{9999}} \\ $$$${Find}\:{the}\:{value}\:{of} \\ $$$$\:\frac{{a}^{\mathrm{4}} }{\left({a}−{b}\right)\left({a}−{c}\right)}+\frac{{b}^{\mathrm{4}} }{\left({b}−{c}\right)\left({b}−{a}\right)}+\frac{{c}^{\mathrm{4}} }{\left({c}−{a}\right)\left({c}−{b}\right)} \\ $$$$ \\ $$
Answered by ajfour last updated on 27/Aug/17
![Let a=pc , b=qc ; then (a^4 /((a−b)(a−c)))+(b^4 /((b−c)(b−a)))+(c^4 /((c−a)(c−b))) =((p^4 c^4 )/(c^2 (p−q)(p−1)))+((q^4 c^4 )/(c^2 (q−1)(q−p))) +(c^4 /(c^2 (1−p)(1−q))) =(c^2 /((p−q)))[(p^4 /(p−1))−(q^4 /(q−1))+((p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((p^4 q−p^4 −pq^4 +q^4 +p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((pq(p^3 −q^3 )−(p^4 −q^4 )+(p−q))/((1−p)(1−q)))] =c^2 [((pq(p^2 +q^2 +pq)−(p^2 +q^2 )(p+q)+1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(pq−p−q)+p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)−p^2 −q^2 +p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)+(p^2 −1)(q^2 −1))/((1−p)(1−q)))] =c^2 [p^2 +q^2 +(p+1)(q+1)] =c^2 [p^2 +q^2 +pq+p+q+1] =a^2 +b^2 +ab+ca+bc+c^2 =(1/2)[(a+b)^2 +(b+c)^2 +(c+a)^2 ] =(1/2)[4×9999+4×99+4×999] =2[9999+999+99] =18[1111+111+11] =18×1233)=9×2466 =22194 . ( option A)](https://www.tinkutara.com/question/Q20500.png)
$${Let}\:{a}={pc}\:,\:\:{b}={qc}\:;\:{then} \\ $$$$\:\frac{{a}^{\mathrm{4}} }{\left({a}−{b}\right)\left({a}−{c}\right)}+\frac{{b}^{\mathrm{4}} }{\left({b}−{c}\right)\left({b}−{a}\right)}+\frac{{c}^{\mathrm{4}} }{\left({c}−{a}\right)\left({c}−{b}\right)} \\ $$$$=\frac{{p}^{\mathrm{4}} {c}^{\mathrm{4}} }{{c}^{\mathrm{2}} \left({p}−{q}\right)\left({p}−\mathrm{1}\right)}+\frac{{q}^{\mathrm{4}} {c}^{\mathrm{4}} }{{c}^{\mathrm{2}} \left({q}−\mathrm{1}\right)\left({q}−{p}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{c}^{\mathrm{4}} }{{c}^{\mathrm{2}} \left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)} \\ $$$$=\frac{{c}^{\mathrm{2}} }{\left({p}−{q}\right)}\left[\frac{{p}^{\mathrm{4}} }{{p}−\mathrm{1}}−\frac{{q}^{\mathrm{4}} }{{q}−\mathrm{1}}+\frac{{p}−{q}}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$=\frac{{c}^{\mathrm{2}} }{\left({p}−{q}\right)}\left[\frac{{p}^{\mathrm{4}} {q}−{p}^{\mathrm{4}} −{pq}^{\mathrm{4}} +{q}^{\mathrm{4}} +{p}−{q}}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$=\frac{{c}^{\mathrm{2}} }{\left({p}−{q}\right)}\left[\frac{{pq}\left({p}^{\mathrm{3}} −{q}^{\mathrm{3}} \right)−\left({p}^{\mathrm{4}} −{q}^{\mathrm{4}} \right)+\left({p}−{q}\right)}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$={c}^{\mathrm{2}} \left[\frac{{pq}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{pq}\right)−\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({p}+{q}\right)+\mathrm{1}}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$={c}^{\mathrm{2}} \left[\frac{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({pq}−{p}−{q}\right)+{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$={c}^{\mathrm{2}} \left[\frac{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({p}−\mathrm{1}\right)\left({q}−\mathrm{1}\right)−{p}^{\mathrm{2}} −{q}^{\mathrm{2}} +{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$={c}^{\mathrm{2}} \left[\frac{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({p}−\mathrm{1}\right)\left({q}−\mathrm{1}\right)+\left({p}^{\mathrm{2}} −\mathrm{1}\right)\left({q}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{1}−{p}\right)\left(\mathrm{1}−{q}\right)}\right] \\ $$$$={c}^{\mathrm{2}} \left[{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\left({p}+\mathrm{1}\right)\left({q}+\mathrm{1}\right)\right] \\ $$$$={c}^{\mathrm{2}} \left[{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{pq}+{p}+{q}+\mathrm{1}\right] \\ $$$$=\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{ab}}+\boldsymbol{{ca}}+\boldsymbol{{bc}}+\boldsymbol{{c}}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} +\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} +\left(\boldsymbol{{c}}+\boldsymbol{{a}}\right)^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{4}×\mathrm{9999}+\mathrm{4}×\mathrm{99}+\mathrm{4}×\mathrm{999}\right] \\ $$$$=\mathrm{2}\left[\mathrm{9999}+\mathrm{999}+\mathrm{99}\right] \\ $$$$=\mathrm{18}\left[\mathrm{1111}+\mathrm{111}+\mathrm{11}\right] \\ $$$$\left.=\mathrm{18}×\mathrm{1233}\right)=\mathrm{9}×\mathrm{2466} \\ $$$$=\mathrm{22194}\:.\:\:\:\left(\:{option}\:{A}\right) \\ $$
