Question Number 20625 by mondodotto@gmail.com last updated on 29/Aug/17
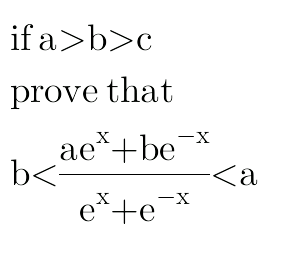
Commented by $@ty@m last updated on 30/Aug/17
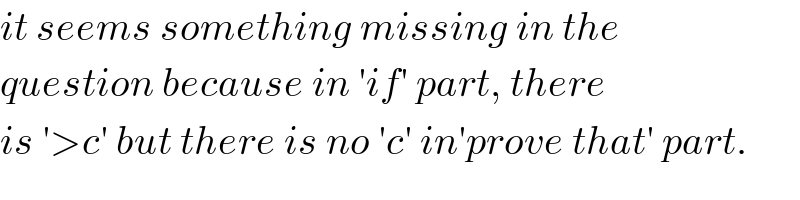
$${it}\:{seems}\:{something}\:{missing}\:{in}\:{the}\: \\ $$$${question}\:{because}\:{in}\:'{if}'\:{part},\:{there} \\ $$$${is}\:'>{c}'\:{but}\:{there}\:{is}\:{no}\:'{c}'\:{in}'{prove}\:{that}'\:{part}. \\ $$
Answered by ajfour last updated on 30/Aug/17
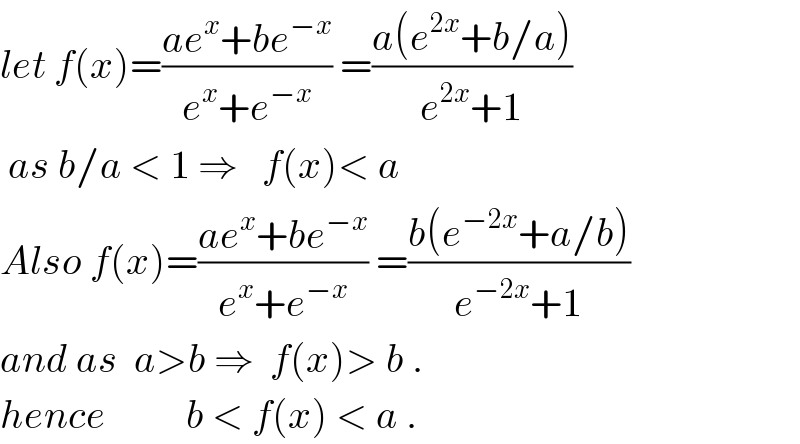
$${let}\:{f}\left({x}\right)=\frac{{ae}^{{x}} +{be}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} }\:=\frac{{a}\left({e}^{\mathrm{2}{x}} +{b}/{a}\right)}{{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$$\:{as}\:{b}/{a}\:<\:\mathrm{1}\:\Rightarrow\:\:\:{f}\left({x}\right)<\:{a} \\ $$$${Also}\:{f}\left({x}\right)=\frac{{ae}^{{x}} +{be}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} }\:=\frac{{b}\left({e}^{−\mathrm{2}{x}} +{a}/{b}\right)}{{e}^{−\mathrm{2}{x}} +\mathrm{1}} \\ $$$${and}\:{as}\:\:{a}>{b}\:\Rightarrow\:\:{f}\left({x}\right)>\:{b}\:. \\ $$$${hence}\:\:\:\:\:\:\:\:\:\:{b}\:<\:{f}\left({x}\right)\:<\:{a}\:. \\ $$
