Question Number 20819 by ajfour last updated on 03/Sep/17
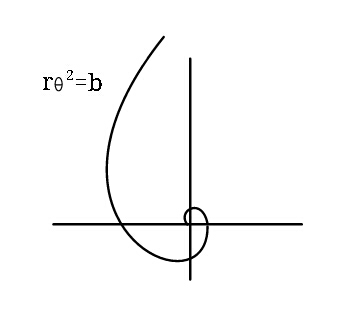
Commented by ajfour last updated on 03/Sep/17
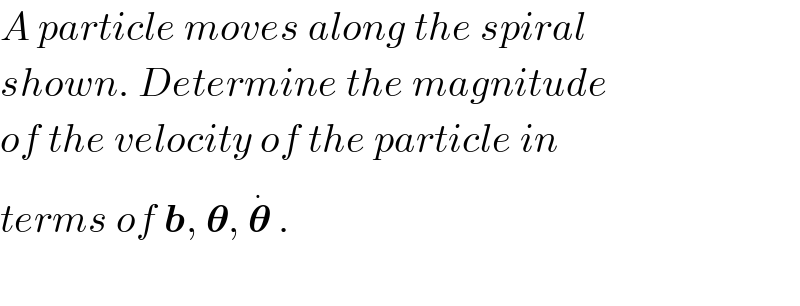
$${A}\:{particle}\:{moves}\:{along}\:{the}\:{spiral} \\ $$$${shown}.\:{Determine}\:{the}\:{magnitude} \\ $$$${of}\:{the}\:{velocity}\:{of}\:{the}\:{particle}\:{in} \\ $$$${terms}\:{of}\:\boldsymbol{{b}},\:\boldsymbol{\theta},\:\overset{.} {\boldsymbol{\theta}}\:. \\ $$$$ \\ $$
Answered by dioph last updated on 04/Sep/17
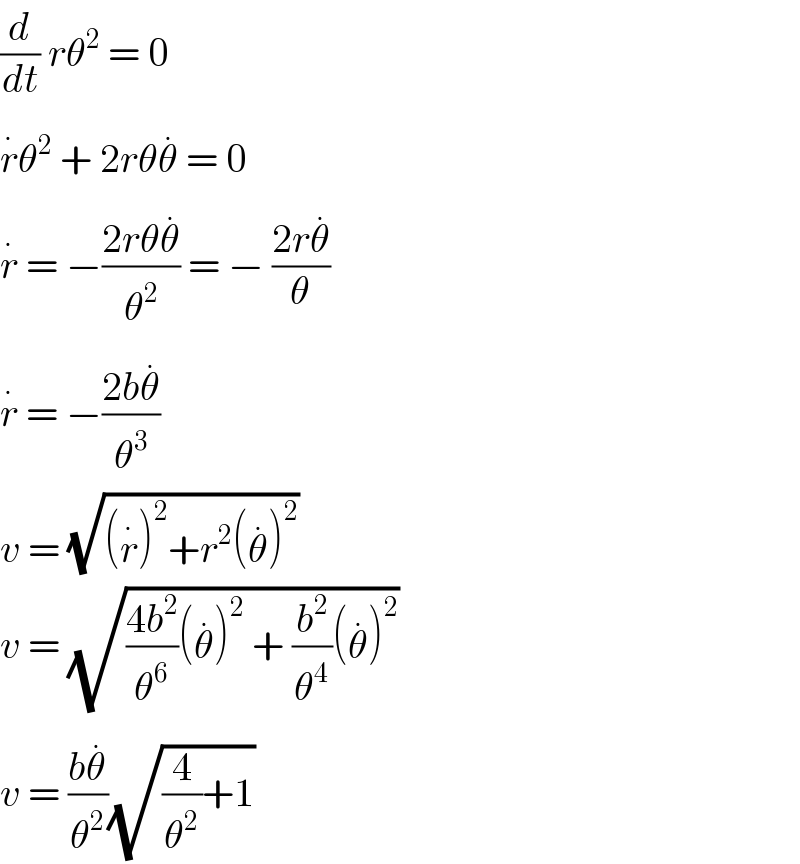
$$\frac{{d}}{{dt}}\:{r}\theta^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\overset{.} {{r}}\theta^{\mathrm{2}} \:+\:\mathrm{2}{r}\theta\overset{.} {\theta}\:=\:\mathrm{0} \\ $$$$\overset{.} {{r}}\:=\:−\frac{\mathrm{2}{r}\theta\overset{.} {\theta}}{\theta^{\mathrm{2}} }\:=\:−\:\frac{\mathrm{2}{r}\overset{.} {\theta}}{\theta} \\ $$$$\overset{.} {{r}}\:=\:−\frac{\mathrm{2}{b}\overset{.} {\theta}}{\theta^{\mathrm{3}} } \\ $$$${v}\:=\:\sqrt{\left(\overset{.} {{r}}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \left(\overset{.} {\theta}\right)^{\mathrm{2}} } \\ $$$${v}\:=\:\sqrt{\frac{\mathrm{4}{b}^{\mathrm{2}} }{\theta^{\mathrm{6}} }\left(\overset{.} {\theta}\right)^{\mathrm{2}} \:+\:\frac{{b}^{\mathrm{2}} }{\theta^{\mathrm{4}} }\left(\overset{.} {\theta}\right)^{\mathrm{2}} } \\ $$$${v}\:=\:\frac{{b}\overset{.} {\theta}}{\theta^{\mathrm{2}} }\sqrt{\frac{\mathrm{4}}{\theta^{\mathrm{2}} }+\mathrm{1}} \\ $$
Commented by ajfour last updated on 04/Sep/17

$${yes}\:{sir},\:{so}\:{it}\:{is}. \\ $$
Commented by ajfour last updated on 04/Sep/17
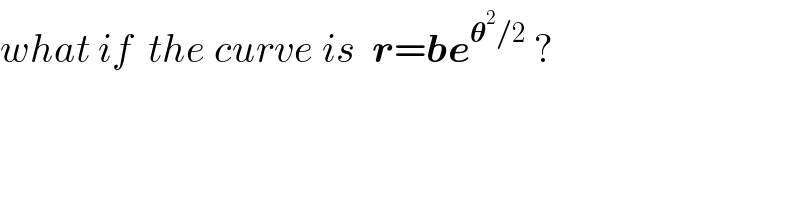
$${what}\:{if}\:\:{the}\:{curve}\:{is}\:\:\boldsymbol{{r}}=\boldsymbol{{be}}^{\boldsymbol{\theta}^{\mathrm{2}} /\mathrm{2}} \:? \\ $$
Commented by dioph last updated on 04/Sep/17
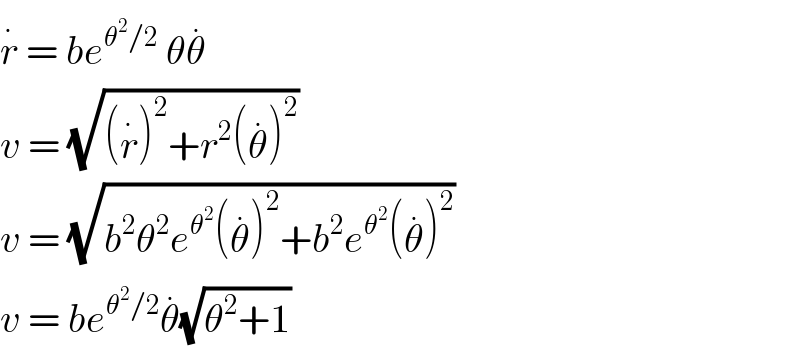
$$\overset{.} {{r}}\:=\:{be}^{\theta^{\mathrm{2}} /\mathrm{2}} \:\theta\overset{.} {\theta} \\ $$$${v}\:=\:\sqrt{\left(\overset{.} {{r}}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \left(\overset{.} {\theta}\right)^{\mathrm{2}} } \\ $$$${v}\:=\:\sqrt{{b}^{\mathrm{2}} \theta^{\mathrm{2}} {e}^{\theta^{\mathrm{2}} } \left(\overset{.} {\theta}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} {e}^{\theta^{\mathrm{2}} } \left(\overset{.} {\theta}\right)^{\mathrm{2}} } \\ $$$${v}\:=\:{be}^{\theta^{\mathrm{2}} /\mathrm{2}} \overset{.} {\theta}\sqrt{\theta^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by dioph last updated on 04/Sep/17

$$\mathrm{indeed},\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{pointing}\:\mathrm{out}. \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{now}\:\mathrm{corrected} \\ $$
