Question Number 20903 by ANTARES_VY last updated on 07/Sep/17
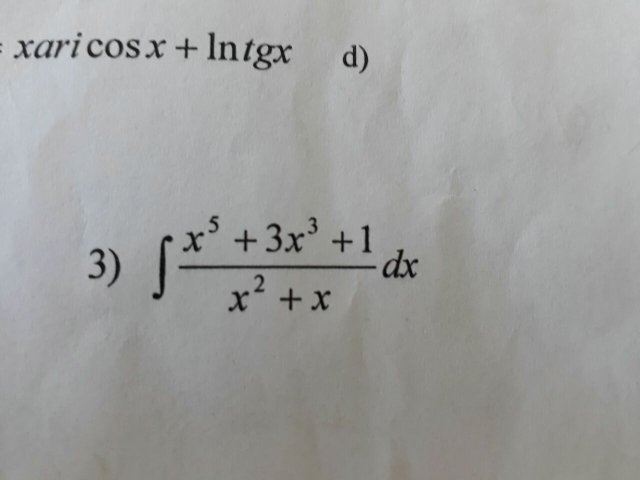
Answered by Joel577 last updated on 07/Sep/17

$$\mathrm{Using}\:\mathrm{polynomial}\:\mathrm{division},\mathrm{we}\:\mathrm{got} \\ $$$${I}\:=\:\int\:{x}^{\mathrm{3}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:−\:\mathrm{4}\:+\:\frac{\mathrm{4}{x}\:+\:\mathrm{1}}{{x}^{\mathrm{2}} \:+\:{x}}\:{dx} \\ $$$$\:\:\:=\:\int\:{x}^{\mathrm{3}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:−\:\mathrm{4}\:{dx}\:+\:\int\:\frac{\mathrm{4}{x}\:+\:\mathrm{1}}{{x}^{\mathrm{2}} \:+\:{x}}\:{dx} \\ $$$$ \\ $$$${P}\:=\:\int\:\frac{\mathrm{4}{x}\:+\:\mathrm{1}}{{x}^{\mathrm{2}} \:+\:{x}}\:{dx}\:=\:\int\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{3}}{{x}\:+\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:\:=\:\mathrm{ln}\:\mid{x}\mid\:+\:\mathrm{3ln}\:\mid{x}\:+\:\mathrm{1}\mid\:+\:{C} \\ $$$$\:\:\:\:=\:\mathrm{ln}\:\mid{x}\left({x}\:+\:\mathrm{1}\right)^{\mathrm{3}} \mid\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} \:−\:\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\:\mathrm{2}{x}^{\mathrm{2}} \:−\:\mathrm{4}{x}\:+\:\mathrm{ln}\:\mid{x}\left({x}\:+\:\mathrm{1}\right)^{\mathrm{3}} \mid\:+\:{C} \\ $$
