Question-20944

Question Number 20944 by tawa tawa last updated on 08/Sep/17

Answered by dioph last updated on 09/Sep/17

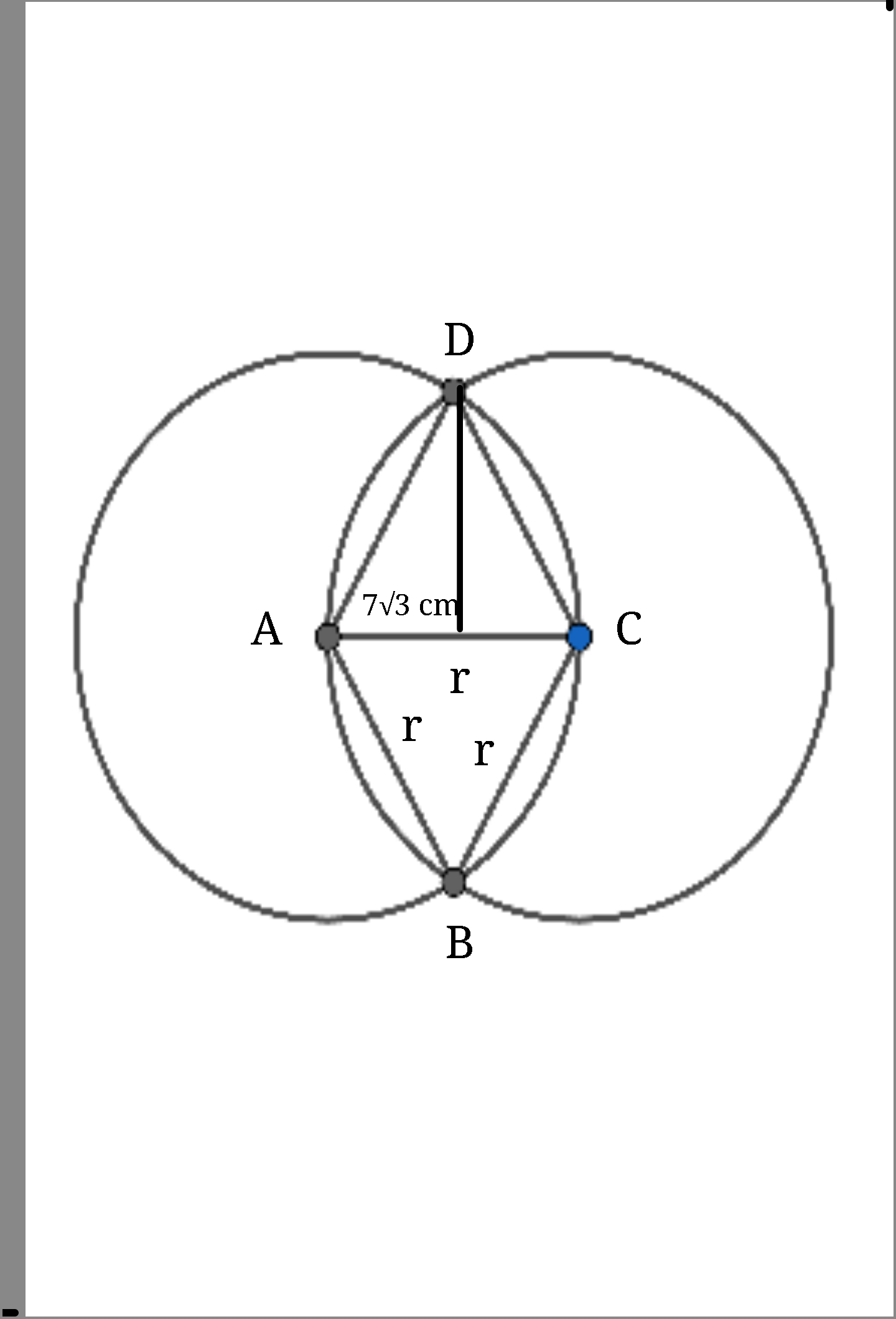
Commented by dioph last updated on 09/Sep/17

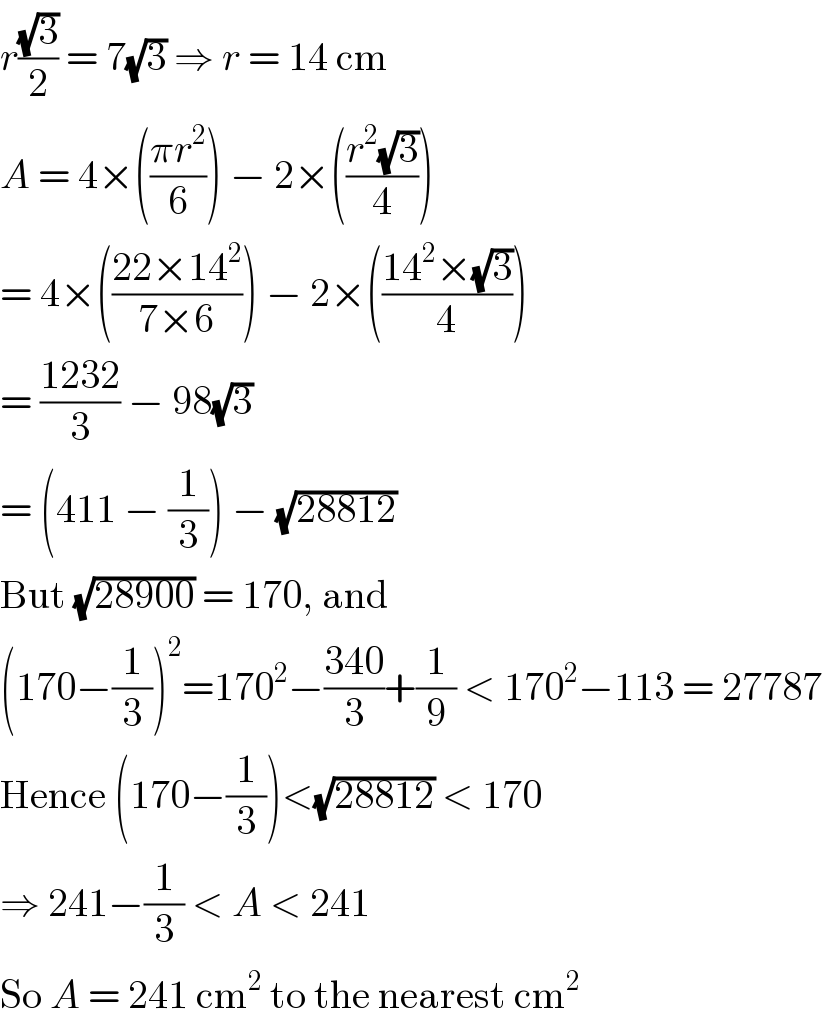
r((√3)/2) = 7(√3) ⇒ r = 14 cm A = 4×(((πr^2 )/6)) − 2×(((r^2 (√3))/4)) = 4×(((22×14^2 )/(7×6))) − 2×(((14^2 ×(√3))/4)) = ((1232)/3) − 98(√3) = (411 − (1/3)) − (√(28812)) But (√(28900)) = 170, and (170−(1/3))^2 =170^2 −((340)/3)+(1/9) < 170^2 −113 = 27787 Hence (170−(1/3))<(√(28812)) < 170 ⇒ 241−(1/3) < A < 241 So A = 241 cm^2 to the nearest cm^2

$${r}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{7}\sqrt{\mathrm{3}}\:\Rightarrow\:{r}\:=\:\mathrm{14}\:\mathrm{cm} \\ $$$${A}\:=\:\mathrm{4}×\left(\frac{\pi{r}^{\mathrm{2}} }{\mathrm{6}}\right)\:−\:\mathrm{2}×\left(\frac{{r}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\:\mathrm{4}×\left(\frac{\mathrm{22}×\mathrm{14}^{\mathrm{2}} }{\mathrm{7}×\mathrm{6}}\right)\:−\:\mathrm{2}×\left(\frac{\mathrm{14}^{\mathrm{2}} ×\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\:\frac{\mathrm{1232}}{\mathrm{3}}\:−\:\mathrm{98}\sqrt{\mathrm{3}} \\ $$$$=\:\left(\mathrm{411}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\right)\:−\:\sqrt{\mathrm{28812}} \\ $$$$\mathrm{But}\:\sqrt{\mathrm{28900}}\:=\:\mathrm{170},\:\mathrm{and} \\ $$$$\left(\mathrm{170}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{170}^{\mathrm{2}} −\frac{\mathrm{340}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}\:<\:\mathrm{170}^{\mathrm{2}} −\mathrm{113}\:=\:\mathrm{27787} \\ $$$$\mathrm{Hence}\:\left(\mathrm{170}−\frac{\mathrm{1}}{\mathrm{3}}\right)<\sqrt{\mathrm{28812}}\:<\:\mathrm{170} \\ $$$$\Rightarrow\:\mathrm{241}−\frac{\mathrm{1}}{\mathrm{3}}\:<\:{A}\:<\:\mathrm{241} \\ $$$$\mathrm{So}\:{A}\:=\:\mathrm{241}\:\mathrm{cm}^{\mathrm{2}} \:\mathrm{to}\:\mathrm{the}\:\mathrm{nearest}\:\mathrm{cm}^{\mathrm{2}} \\ $$

Commented by tawa tawa last updated on 10/Sep/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply