Question-20992

Question Number 20992 by NECx last updated on 09/Sep/17

Commented by NECx last updated on 09/Sep/17

$$\mathrm{please}\:\mathrm{help}\:\mathrm{guys} \\ $$

Answered by $@ty@m last updated on 10/Sep/17

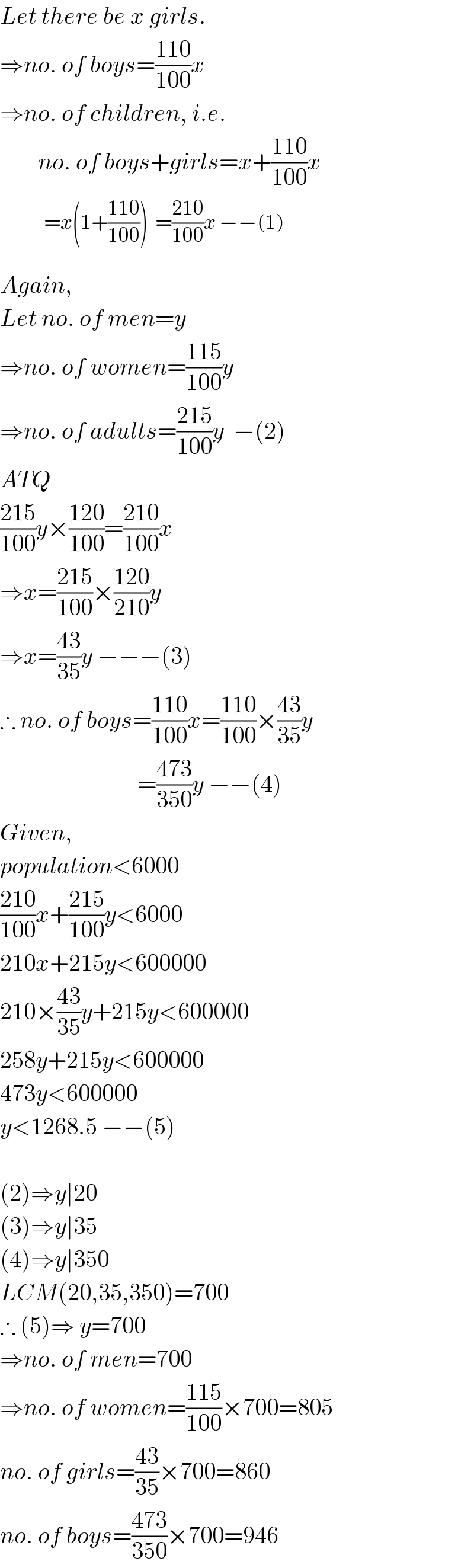
Let there be x girls. ⇒no. of boys=((110)/(100))x ⇒no. of children, i.e. no. of boys+girls=x+((110)/(100))x Again, Let no. of men=y ⇒no. of women=((115)/(100))y ⇒no. of adults=((215)/(100))y −(2) ATQ ((215)/(100))y×((120)/(100))=((210)/(100))x ⇒x=((215)/(100))×((120)/(210))y ⇒x=((43)/(35))y −−−(3) ∴ no. of boys=((110)/(100))x=((110)/(100))×((43)/(35))y =((473)/(350))y −−(4) Given, population<6000 ((210)/(100))x+((215)/(100))y<6000 210x+215y<600000 210×((43)/(35))y+215y<600000 258y+215y<600000 473y<600000 y<1268.5 −−(5) (2)⇒y∣20 (3)⇒y∣35 (4)⇒y∣350 LCM(20,35,350)=700 ∴ (5)⇒ y=700 ⇒no. of men=700 ⇒no. of women=((115)/(100))×700=805 no. of girls=((43)/(35))×700=860 no. of boys=((473)/(350))×700=946

$${Let}\:{there}\:{be}\:{x}\:{girls}. \\ $$$$\Rightarrow{no}.\:{of}\:{boys}=\frac{\mathrm{110}}{\mathrm{100}}{x} \\ $$$$\Rightarrow{no}.\:{of}\:{children},\:{i}.{e}. \\ $$$$\:\:\:\:\:\:\:\:{no}.\:{of}\:{boys}+{girls}={x}+\frac{\mathrm{110}}{\mathrm{100}}{x} \\ $$$$\:\:\:\:\: \\ $$$${Again}, \\ $$$${Let}\:{no}.\:{of}\:{men}={y} \\ $$$$\Rightarrow{no}.\:{of}\:{women}=\frac{\mathrm{115}}{\mathrm{100}}{y}\: \\ $$$$\Rightarrow{no}.\:{of}\:{adults}=\frac{\mathrm{215}}{\mathrm{100}}{y}\:\:−\left(\mathrm{2}\right) \\ $$$${ATQ} \\ $$$$\frac{\mathrm{215}}{\mathrm{100}}{y}×\frac{\mathrm{120}}{\mathrm{100}}=\frac{\mathrm{210}}{\mathrm{100}}{x} \\ $$$$\Rightarrow{x}=\frac{\mathrm{215}}{\mathrm{100}}×\frac{\mathrm{120}}{\mathrm{210}}{y} \\ $$$$\Rightarrow{x}=\frac{\mathrm{43}}{\mathrm{35}}{y}\:−−−\left(\mathrm{3}\right) \\ $$$$\therefore\:{no}.\:{of}\:{boys}=\frac{\mathrm{110}}{\mathrm{100}}{x}=\frac{\mathrm{110}}{\mathrm{100}}×\frac{\mathrm{43}}{\mathrm{35}}{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{473}}{\mathrm{350}}{y}\:−−\left(\mathrm{4}\right) \\ $$$${Given}, \\ $$$${population}<\mathrm{6000} \\ $$$$\frac{\mathrm{210}}{\mathrm{100}}{x}+\frac{\mathrm{215}}{\mathrm{100}}{y}<\mathrm{6000} \\ $$$$\mathrm{210}{x}+\mathrm{215}{y}<\mathrm{600000} \\ $$$$\mathrm{210}×\frac{\mathrm{43}}{\mathrm{35}}{y}+\mathrm{215}{y}<\mathrm{600000} \\ $$$$\mathrm{258}{y}+\mathrm{215}{y}<\mathrm{600000} \\ $$$$\mathrm{473}{y}<\mathrm{600000} \\ $$$${y}<\mathrm{1268}.\mathrm{5}\:−−\left(\mathrm{5}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\Rightarrow{y}\mid\mathrm{20} \\ $$$$\left(\mathrm{3}\right)\Rightarrow{y}\mid\mathrm{35} \\ $$$$\left(\mathrm{4}\right)\Rightarrow{y}\mid\mathrm{350} \\ $$$${LCM}\left(\mathrm{20},\mathrm{35},\mathrm{350}\right)=\mathrm{700} \\ $$$$\therefore\:\left(\mathrm{5}\right)\Rightarrow\:{y}=\mathrm{700} \\ $$$$\Rightarrow{no}.\:{of}\:{men}=\mathrm{700} \\ $$$$\Rightarrow{no}.\:{of}\:{women}=\frac{\mathrm{115}}{\mathrm{100}}×\mathrm{700}=\mathrm{805} \\ $$$${no}.\:{of}\:{girls}=\frac{\mathrm{43}}{\mathrm{35}}×\mathrm{700}=\mathrm{860} \\ $$$${no}.\:{of}\:{boys}=\frac{\mathrm{473}}{\mathrm{350}}×\mathrm{700}=\mathrm{946} \\ $$

Commented by NECx last updated on 10/Sep/17

wow..... this is great sir. i′m most grateful sir.Words cant express how happy I am. Thank you

$$\mathrm{wow}…..\:\mathrm{this}\:\mathrm{is}\:\mathrm{great}\:\mathrm{sir}. \\ $$$$\mathrm{i}'\mathrm{m}\:\mathrm{most}\:\mathrm{grateful}\:\mathrm{sir}.\mathrm{Words}\:\mathrm{cant} \\ $$$$\mathrm{express}\:\mathrm{how}\:\mathrm{happy}\:\mathrm{I}\:\mathrm{am}.\:\mathrm{Thank} \\ $$$$\mathrm{you} \\ $$

Commented by NECx last updated on 10/Sep/17

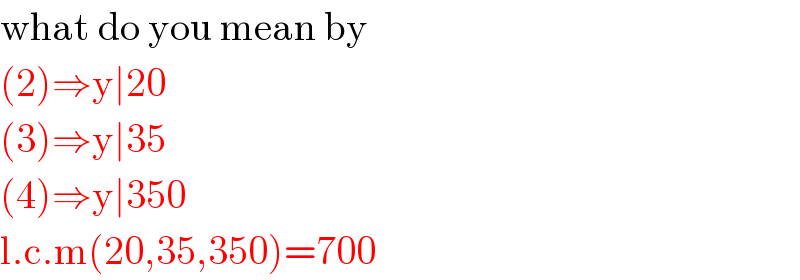
what do you mean by (2)⇒y∣20 (3)⇒y∣35 (4)⇒y∣350 l.c.m(20,35,350)=700

$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{by} \\ $$$$\left(\mathrm{2}\right)\Rightarrow\mathrm{y}\mid\mathrm{20} \\ $$$$\left(\mathrm{3}\right)\Rightarrow\mathrm{y}\mid\mathrm{35} \\ $$$$\left(\mathrm{4}\right)\Rightarrow\mathrm{y}\mid\mathrm{350} \\ $$$$\mathrm{l}.\mathrm{c}.\mathrm{m}\left(\mathrm{20},\mathrm{35},\mathrm{350}\right)=\mathrm{700} \\ $$

Commented by $@ty@m last updated on 10/Sep/17

∵ y is no. of men ∴y∈N Similarly no. of adults=((215)/(100))y∈N which is possible only if y is a multiple of 20. that is what I meant by (2)⇒y∣20 and likewise for other two expessions. Further, to fulfill the three conditions simltaneously we′ll have to find the Least Common Multiple (LCM) of 20, 35 and 350 which is 700. ∴y∈{700, 1400, ......} but in ineqation(5), we have y<1268.5 ⇒y=700 Are all your doubts clear now?

$$\because\:{y}\:{is}\:{no}.\:{of}\:{men} \\ $$$$\therefore{y}\in\mathrm{N} \\ $$$$\:{Similarly}\:{no}.\:{of}\:{adults}=\frac{\mathrm{215}}{\mathrm{100}}{y}\in\mathrm{N} \\ $$$${which}\:{is}\:{possible}\:{only}\:{if}\:{y}\:{is}\:{a}\:{multiple}\:{of}\:\mathrm{20}. \\ $$$${that}\:{is}\:{what}\:{I}\:{meant}\:{by}\: \\ $$$$\left(\mathrm{2}\right)\Rightarrow\mathrm{y}\mid\mathrm{20}\: \\ $$$${and}\:{likewise}\:{for}\:{other}\:{two}\:{expessions}. \\ $$$${Further},\:{to}\:{fulfill}\:{the}\:{three}\: \\ $$$${conditions}\:{simltaneously} \\ $$$${we}'{ll}\:{have}\:{to}\:{find}\:{the}\:{Least}\:{Common} \\ $$$${Multiple}\:\left({LCM}\right)\:{of}\:\mathrm{20},\:\mathrm{35}\:{and}\:\mathrm{350} \\ $$$${which}\:{is}\:\mathrm{700}. \\ $$$$\therefore{y}\in\left\{\mathrm{700},\:\mathrm{1400},\:……\right\} \\ $$$${but}\:{in}\:{ineqation}\left(\mathrm{5}\right),\:{we}\:{have} \\ $$$${y}<\mathrm{1268}.\mathrm{5} \\ $$$$\Rightarrow{y}=\mathrm{700} \\ $$$${Are}\:{all}\:{your}\:{doubts}\:{clear}\:{now}? \\ $$

Commented by NECx last updated on 10/Sep/17

yeah.... i understand . please which topic in maths does this question come from?

$$\mathrm{yeah}….\:\mathrm{i}\:\mathrm{understand}\:. \\ $$$$\mathrm{please}\:\mathrm{which}\:\mathrm{topic}\:\mathrm{in}\:\mathrm{maths}\:\mathrm{does} \\ $$$$\mathrm{this}\:\mathrm{question}\:\mathrm{come}\:\mathrm{from}? \\ $$

Commented by $@ty@m last updated on 10/Sep/17

$${HaaHaaHaa} \\ $$$${the}\:{same}\:{question}\:{I}\:{was}\:{going} \\ $$$${to}\:{ask}\:{you}…. \\ $$$${It}\:{seems}\:{to}\:{be}\:“{Applcation}\:{of}\:{ineqality}'' \\ $$$${but}\:{actually}\:{perception}\:{of}\:“{Percentage}''\:{and} \\ $$$$“{Number}\:{Theory}''\:{are}\:{also}\:{involved}. \\ $$$${More}\:{than}\:{theory},\:{it}\:{needs}\:{logic} \\ $$$${to}\:{solve}. \\ $$

Commented by NECx last updated on 10/Sep/17

$$\mathrm{hmmmm}….\:\mathrm{i}\:\mathrm{hear}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by mrW1 last updated on 10/Sep/17

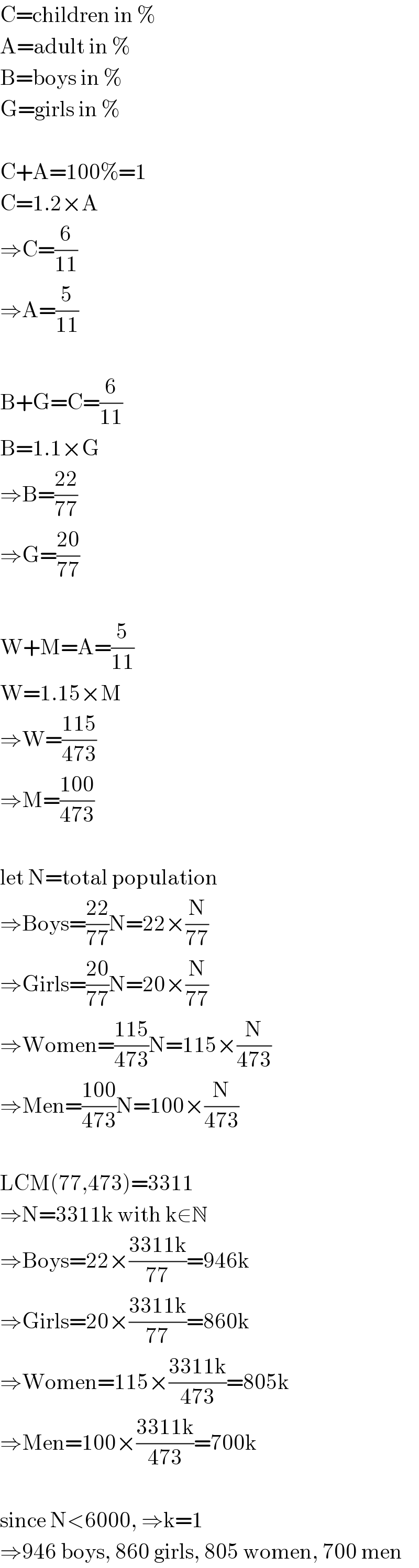
C=children in % A=adult in % B=boys in % G=girls in % C+A=100%=1 C=1.2×A ⇒C=(6/(11)) ⇒A=(5/(11)) B+G=C=(6/(11)) B=1.1×G ⇒B=((22)/(77)) ⇒G=((20)/(77)) W+M=A=(5/(11)) W=1.15×M ⇒W=((115)/(473)) ⇒M=((100)/(473)) let N=total population ⇒Boys=((22)/(77))N=22×(N/(77)) ⇒Girls=((20)/(77))N=20×(N/(77)) ⇒Women=((115)/(473))N=115×(N/(473)) ⇒Men=((100)/(473))N=100×(N/(473)) LCM(77,473)=3311 ⇒N=3311k with k∈N ⇒Boys=22×((3311k)/(77))=946k ⇒Girls=20×((3311k)/(77))=860k ⇒Women=115×((3311k)/(473))=805k ⇒Men=100×((3311k)/(473))=700k since N<6000, ⇒k=1 ⇒946 boys, 860 girls, 805 women, 700 men

$$\mathrm{C}=\mathrm{children}\:\mathrm{in}\:\% \\ $$$$\mathrm{A}=\mathrm{adult}\:\mathrm{in}\:\% \\ $$$$\mathrm{B}=\mathrm{boys}\:\mathrm{in}\:\% \\ $$$$\mathrm{G}=\mathrm{girls}\:\mathrm{in}\:\% \\ $$$$ \\ $$$$\mathrm{C}+\mathrm{A}=\mathrm{100\%}=\mathrm{1} \\ $$$$\mathrm{C}=\mathrm{1}.\mathrm{2}×\mathrm{A} \\ $$$$\Rightarrow\mathrm{C}=\frac{\mathrm{6}}{\mathrm{11}} \\ $$$$\Rightarrow\mathrm{A}=\frac{\mathrm{5}}{\mathrm{11}} \\ $$$$ \\ $$$$\mathrm{B}+\mathrm{G}=\mathrm{C}=\frac{\mathrm{6}}{\mathrm{11}} \\ $$$$\mathrm{B}=\mathrm{1}.\mathrm{1}×\mathrm{G} \\ $$$$\Rightarrow\mathrm{B}=\frac{\mathrm{22}}{\mathrm{77}} \\ $$$$\Rightarrow\mathrm{G}=\frac{\mathrm{20}}{\mathrm{77}} \\ $$$$ \\ $$$$\mathrm{W}+\mathrm{M}=\mathrm{A}=\frac{\mathrm{5}}{\mathrm{11}} \\ $$$$\mathrm{W}=\mathrm{1}.\mathrm{15}×\mathrm{M} \\ $$$$\Rightarrow\mathrm{W}=\frac{\mathrm{115}}{\mathrm{473}} \\ $$$$\Rightarrow\mathrm{M}=\frac{\mathrm{100}}{\mathrm{473}} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{N}=\mathrm{total}\:\mathrm{population} \\ $$$$\Rightarrow\mathrm{Boys}=\frac{\mathrm{22}}{\mathrm{77}}\mathrm{N}=\mathrm{22}×\frac{\mathrm{N}}{\mathrm{77}} \\ $$$$\Rightarrow\mathrm{Girls}=\frac{\mathrm{20}}{\mathrm{77}}\mathrm{N}=\mathrm{20}×\frac{\mathrm{N}}{\mathrm{77}} \\ $$$$\Rightarrow\mathrm{Women}=\frac{\mathrm{115}}{\mathrm{473}}\mathrm{N}=\mathrm{115}×\frac{\mathrm{N}}{\mathrm{473}} \\ $$$$\Rightarrow\mathrm{Men}=\frac{\mathrm{100}}{\mathrm{473}}\mathrm{N}=\mathrm{100}×\frac{\mathrm{N}}{\mathrm{473}} \\ $$$$ \\ $$$$\mathrm{LCM}\left(\mathrm{77},\mathrm{473}\right)=\mathrm{3311} \\ $$$$\Rightarrow\mathrm{N}=\mathrm{3311k}\:\mathrm{with}\:\mathrm{k}\in\mathbb{N} \\ $$$$\Rightarrow\mathrm{Boys}=\mathrm{22}×\frac{\mathrm{3311k}}{\mathrm{77}}=\mathrm{946k} \\ $$$$\Rightarrow\mathrm{Girls}=\mathrm{20}×\frac{\mathrm{3311k}}{\mathrm{77}}=\mathrm{860k} \\ $$$$\Rightarrow\mathrm{Women}=\mathrm{115}×\frac{\mathrm{3311k}}{\mathrm{473}}=\mathrm{805k} \\ $$$$\Rightarrow\mathrm{Men}=\mathrm{100}×\frac{\mathrm{3311k}}{\mathrm{473}}=\mathrm{700k} \\ $$$$ \\ $$$$\mathrm{since}\:\mathrm{N}<\mathrm{6000},\:\Rightarrow\mathrm{k}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{946}\:\mathrm{boys},\:\mathrm{860}\:\mathrm{girls},\:\mathrm{805}\:\mathrm{women},\:\mathrm{700}\:\mathrm{men} \\ $$

Commented by NECx last updated on 10/Sep/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by NECx last updated on 10/Sep/17

sorry but i really need to ask this; why was it necessary to find the LCM of the denominators? Thanks for always helping.

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{i}\:\mathrm{really}\:\mathrm{need}\:\mathrm{to}\:\mathrm{ask}\:\mathrm{this}; \\ $$$$ \\ $$$$\mathrm{why}\:\mathrm{was}\:\mathrm{it}\:\mathrm{necessary}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{LCM}\:\mathrm{of}\:\mathrm{the}\:\mathrm{denominators}? \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{always}\:\mathrm{helping}. \\ $$

Commented by mrW1 last updated on 11/Sep/17

(N/(77)) and (N/(473)) must be integer, i.e. N must be a multiple of 77 and 473. ⇒N=LCM(77,473)×k=3311k

$$\frac{\mathrm{N}}{\mathrm{77}}\:\mathrm{and}\:\frac{\mathrm{N}}{\mathrm{473}}\:\mathrm{must}\:\mathrm{be}\:\mathrm{integer},\:\mathrm{i}.\mathrm{e}. \\ $$$$\mathrm{N}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{77}\:\mathrm{and}\:\mathrm{473}. \\ $$$$\Rightarrow\mathrm{N}=\mathrm{LCM}\left(\mathrm{77},\mathrm{473}\right)×\mathrm{k}=\mathrm{3311k} \\ $$

Answered by ajfour last updated on 10/Sep/17

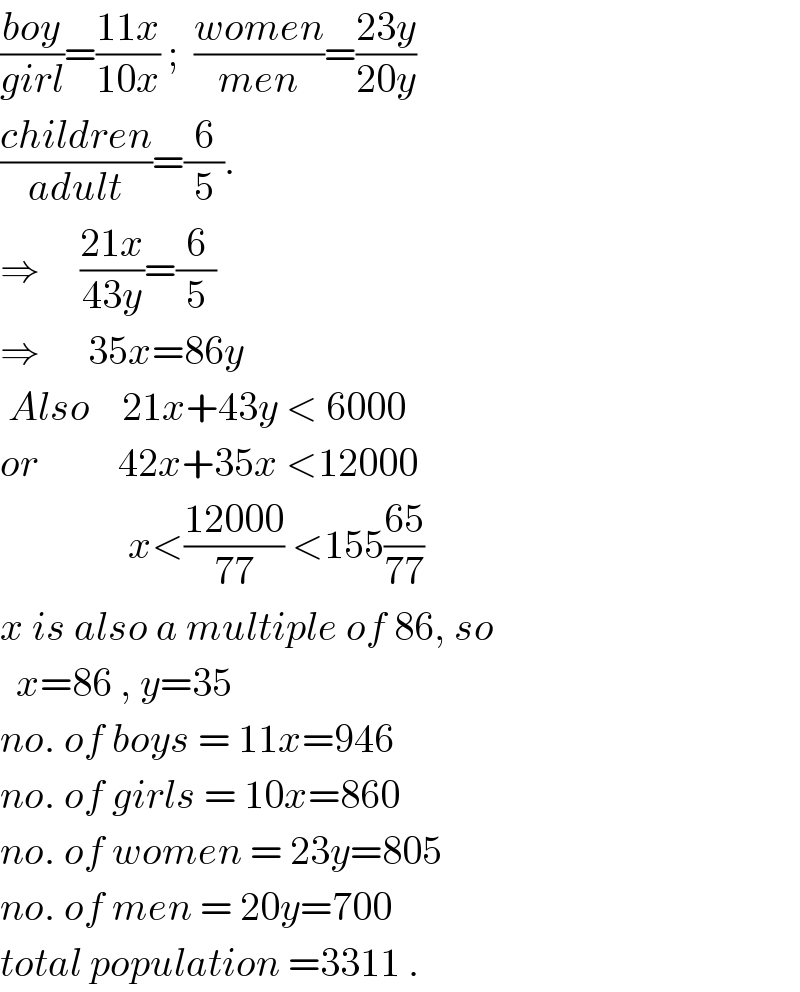
((boy)/(girl))=((11x)/(10x)) ; ((women)/(men))=((23y)/(20y)) ((children)/(adult))=(6/5). ⇒ ((21x)/(43y))=(6/5) ⇒ 35x=86y Also 21x+43y < 6000 or 42x+35x <12000 x<((12000)/(77)) <155((65)/(77)) x is also a multiple of 86, so x=86 , y=35 no. of boys = 11x=946 no. of girls = 10x=860 no. of women = 23y=805 no. of men = 20y=700 total population =3311 .

$$\frac{{boy}}{{girl}}=\frac{\mathrm{11}{x}}{\mathrm{10}{x}}\:;\:\:\frac{{women}}{{men}}=\frac{\mathrm{23}{y}}{\mathrm{20}{y}} \\ $$$$\frac{{children}}{{adult}}=\frac{\mathrm{6}}{\mathrm{5}}. \\ $$$$\Rightarrow\:\:\:\:\:\frac{\mathrm{21}{x}}{\mathrm{43}{y}}=\frac{\mathrm{6}}{\mathrm{5}}\: \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{35}{x}=\mathrm{86}{y} \\ $$$$\:{Also}\:\:\:\:\mathrm{21}{x}+\mathrm{43}{y}\:<\:\mathrm{6000} \\ $$$${or}\:\:\:\:\:\:\:\:\:\:\mathrm{42}{x}+\mathrm{35}{x}\:<\mathrm{12000} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}<\frac{\mathrm{12000}}{\mathrm{77}}\:<\mathrm{155}\frac{\mathrm{65}}{\mathrm{77}} \\ $$$${x}\:{is}\:{also}\:{a}\:{multiple}\:{of}\:\mathrm{86},\:{so} \\ $$$$\:\:{x}=\mathrm{86}\:,\:{y}=\mathrm{35} \\ $$$${no}.\:{of}\:{boys}\:=\:\mathrm{11}{x}=\mathrm{946} \\ $$$${no}.\:{of}\:{girls}\:=\:\mathrm{10}{x}=\mathrm{860} \\ $$$${no}.\:{of}\:{women}\:=\:\mathrm{23}{y}=\mathrm{805} \\ $$$${no}.\:{of}\:{men}\:=\:\mathrm{20}{y}=\mathrm{700} \\ $$$${total}\:{population}\:=\mathrm{3311}\:. \\ $$

Commented by NECx last updated on 10/Sep/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by $@ty@m last updated on 10/Sep/17

$$\mathbb{BEST}\:\mathbb{SOLUTION} \\ $$

Commented by NECx last updated on 10/Sep/17

seems to be a really nice solution for others but i′m really confused. This is my question here guys , 35x=86y .....how?

$$\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{a}\:\mathrm{really}\:\mathrm{nice}\:\mathrm{solution} \\ $$$$\mathrm{for}\:\mathrm{others}\:\mathrm{but}\:\mathrm{i}'\mathrm{m}\:\mathrm{really}\:\mathrm{confused}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{my}\:\mathrm{question}\:\mathrm{here}\:\mathrm{guys}\:, \\ $$$$\mathrm{35x}=\mathrm{86y}\:\:\:\:\:\:\:\:…..\mathrm{how}? \\ $$

Commented by ajfour last updated on 11/Sep/17

$${follows}\:{from}\:{line}\:{before}\:.. \\ $$

Commented by NECx last updated on 11/Sep/17

$$\mathrm{oh}…\:\mathrm{its}\:\mathrm{clear} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply