Question Number 21009 by xxyy@gmail.com last updated on 10/Sep/17
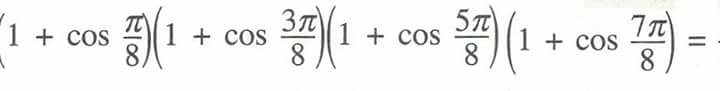
Answered by Tinkutara last updated on 10/Sep/17
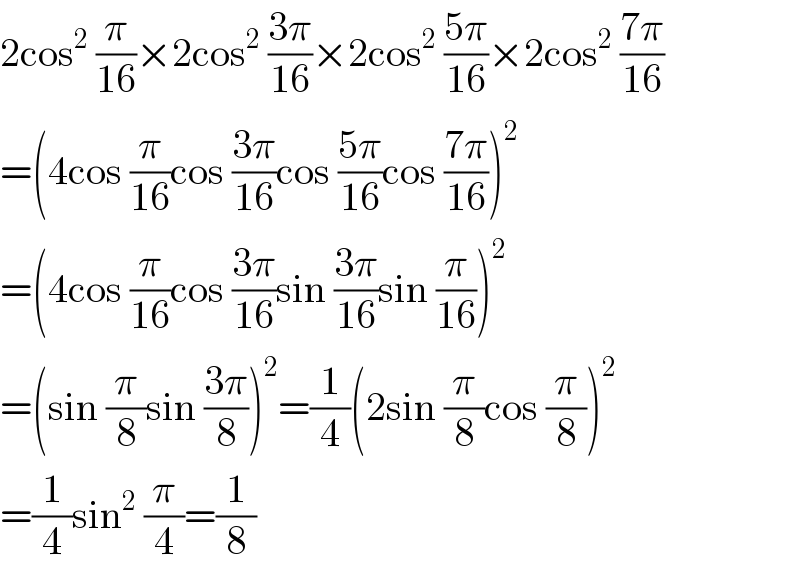
$$\mathrm{2cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{16}}×\mathrm{2cos}^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{16}}×\mathrm{2cos}^{\mathrm{2}} \:\frac{\mathrm{5}\pi}{\mathrm{16}}×\mathrm{2cos}^{\mathrm{2}} \:\frac{\mathrm{7}\pi}{\mathrm{16}} \\ $$$$=\left(\mathrm{4cos}\:\frac{\pi}{\mathrm{16}}\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{16}}\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{16}}\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{16}}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{4cos}\:\frac{\pi}{\mathrm{16}}\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{16}}\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{16}}\mathrm{sin}\:\frac{\pi}{\mathrm{16}}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{sin}\:\frac{\pi}{\mathrm{8}}\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2sin}\:\frac{\pi}{\mathrm{8}}\mathrm{cos}\:\frac{\pi}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \:\frac{\pi}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by xxyy@gmail.com last updated on 10/Sep/17

$$\mathrm{thank}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}! \\ $$
