Question Number 21038 by ajfour last updated on 10/Sep/17
Commented by ajfour last updated on 10/Sep/17

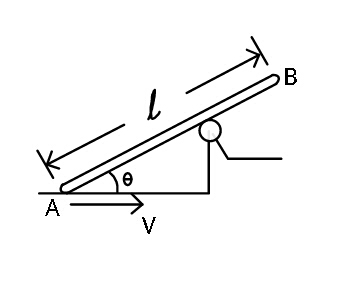
$${Find}\:{angular}\:{velocity}\:{and}\:{angular} \\ $$$${acceleration}\:{of}\:{rod}\:{if}\:{end}\:{A}\:{moves} \\ $$$${to}\:{the}\:{right}\:{with}\:{constant}\:{velocity} \\ $$$${v}. \\ $$
Answered by mrW1 last updated on 11/Sep/17
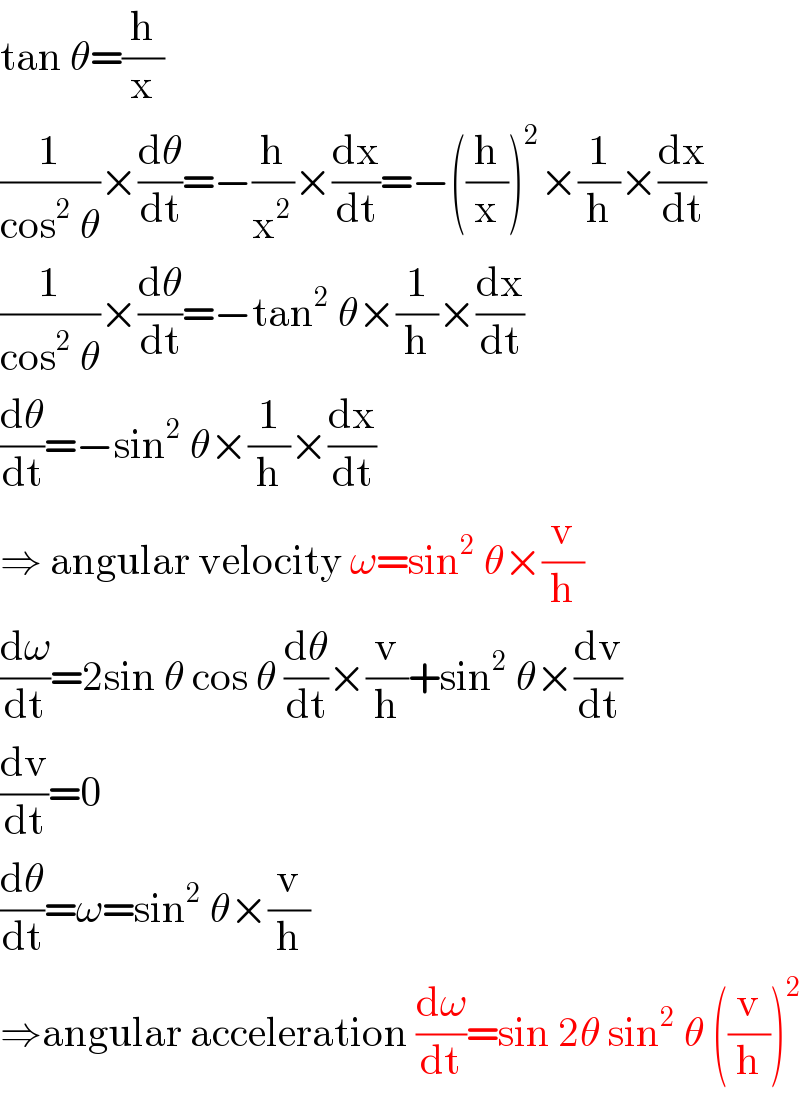
$$\mathrm{tan}\:\theta=\frac{\mathrm{h}}{\mathrm{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}×\frac{\mathrm{d}\theta}{\mathrm{dt}}=−\frac{\mathrm{h}}{\mathrm{x}^{\mathrm{2}} }×\frac{\mathrm{dx}}{\mathrm{dt}}=−\left(\frac{\mathrm{h}}{\mathrm{x}}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{h}}×\frac{\mathrm{dx}}{\mathrm{dt}} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}×\frac{\mathrm{d}\theta}{\mathrm{dt}}=−\mathrm{tan}^{\mathrm{2}} \:\theta×\frac{\mathrm{1}}{\mathrm{h}}×\frac{\mathrm{dx}}{\mathrm{dt}} \\ $$$$\frac{\mathrm{d}\theta}{\mathrm{dt}}=−\mathrm{sin}^{\mathrm{2}} \:\theta×\frac{\mathrm{1}}{\mathrm{h}}×\frac{\mathrm{dx}}{\mathrm{dt}} \\ $$$$\Rightarrow\:\mathrm{angular}\:\mathrm{velocity}\:\omega=\mathrm{sin}^{\mathrm{2}} \:\theta×\frac{\mathrm{v}}{\mathrm{h}} \\ $$$$\frac{\mathrm{d}\omega}{\mathrm{dt}}=\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\:\frac{\mathrm{d}\theta}{\mathrm{dt}}×\frac{\mathrm{v}}{\mathrm{h}}+\mathrm{sin}^{\mathrm{2}} \:\theta×\frac{\mathrm{dv}}{\mathrm{dt}} \\ $$$$\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{0} \\ $$$$\frac{\mathrm{d}\theta}{\mathrm{dt}}=\omega=\mathrm{sin}^{\mathrm{2}} \:\theta×\frac{\mathrm{v}}{\mathrm{h}} \\ $$$$\Rightarrow\mathrm{angular}\:\mathrm{acceleration}\:\frac{\mathrm{d}\omega}{\mathrm{dt}}=\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}^{\mathrm{2}} \:\theta\:\left(\frac{\mathrm{v}}{\mathrm{h}}\right)^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 11/Sep/17

$${thanks}\:{sir},{i}\:{had}\:{missed}\:{marking}\: \\ $$$$\boldsymbol{{h}}\:{in}\:{question},\:{thanks}\:{for} \\ $$$${assuming}\:{so}\:{and}\:{solving}\:{perfectly}. \\ $$
