Question-21394

Question Number 21394 by mondodotto@gmail.com last updated on 22/Sep/17

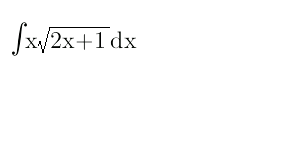
Answered by mrW1 last updated on 22/Sep/17

t=(√(2x+1)) x=((t^2 −1)/2) dx=tdt ∫x(√(2x+1)) dx=∫((t^2 −1)/2)×t×tdt =(1/2)∫(t^4 −t^2 )dt =(t^5 /(10))−(t^3 /6)+C =(t^3 /2)((t^2 /5)−(1/3))+C =(((2x+1)(√(2x+1)))/2)[((2x+1)/5)−(1/3)]+C =(((3x−1)(2x+1)(√(2x+1)))/(15))+C

$$\mathrm{t}=\sqrt{\mathrm{2x}+\mathrm{1}} \\ $$$$\mathrm{x}=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{dx}=\mathrm{tdt} \\ $$$$\int\mathrm{x}\sqrt{\mathrm{2x}+\mathrm{1}}\:\mathrm{dx}=\int\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}×\mathrm{t}×\mathrm{tdt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{t}^{\mathrm{4}} −\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\frac{\mathrm{t}^{\mathrm{5}} }{\mathrm{10}}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}+\mathrm{C} \\ $$$$=\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{2}}\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{C} \\ $$$$=\frac{\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{2x}+\mathrm{1}}}{\mathrm{2}}\left[\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}\right]+\mathrm{C} \\ $$$$=\frac{\left(\mathrm{3x}−\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{2x}+\mathrm{1}}}{\mathrm{15}}+\mathrm{C} \\ $$

Answered by sma3l2996 last updated on 22/Sep/17

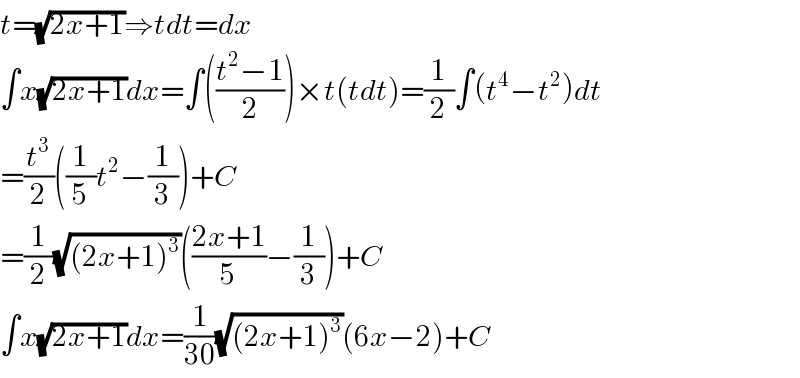
t=(√(2x+1))⇒tdt=dx ∫x(√(2x+1))dx=∫(((t^2 −1)/2))×t(tdt)=(1/2)∫(t^4 −t^2 )dt =(t^3 /2)((1/5)t^2 −(1/3))+C =(1/2)(√((2x+1)^3 ))(((2x+1)/5)−(1/3))+C ∫x(√(2x+1))dx=(1/(30))(√((2x+1)^3 ))(6x−2)+C

$${t}=\sqrt{\mathrm{2}{x}+\mathrm{1}}\Rightarrow{tdt}={dx} \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}{dx}=\int\left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right)×{t}\left({tdt}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$=\frac{{t}^{\mathrm{3}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{5}}{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} }\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+{C} \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{30}}\sqrt{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} }\left(\mathrm{6}{x}−\mathrm{2}\right)+{C} \\ $$

Commented by edward last updated on 23/Sep/17

$$\:{Kigundus}\:{checks}\:{papa} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply