Question Number 21566 by mondodotto@gmail.com last updated on 27/Sep/17

Commented by mrW1 last updated on 27/Sep/17

$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{2} \\ $$
Commented by FilupS last updated on 27/Sep/17
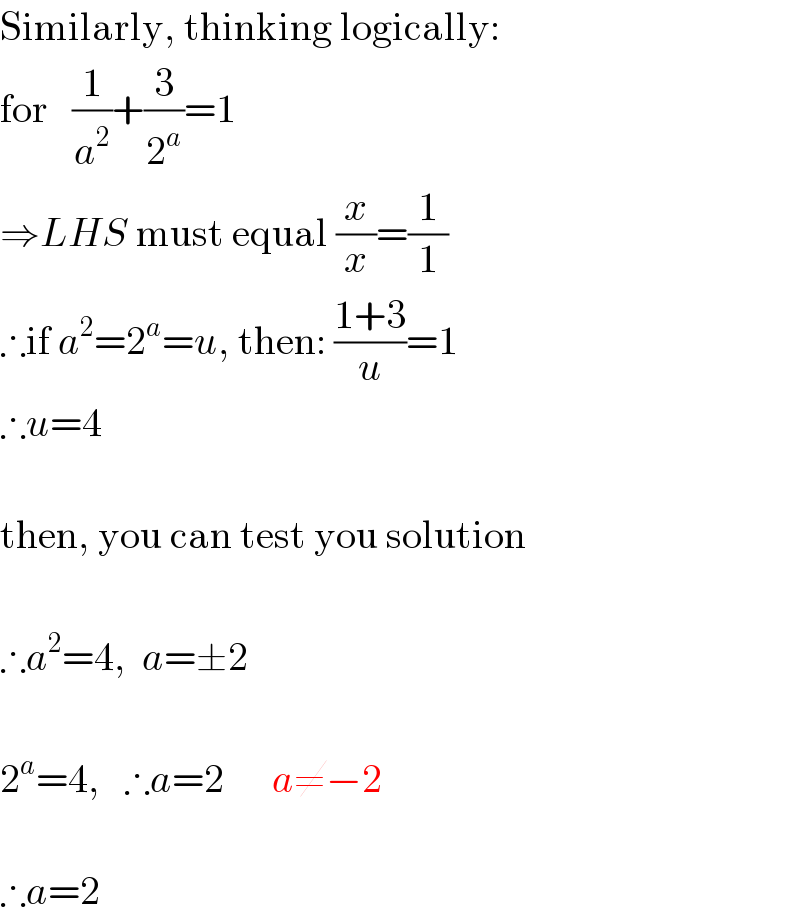
$$\mathrm{Similarly},\:\mathrm{thinking}\:\mathrm{logically}: \\ $$$$\mathrm{for}\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{{a}} }=\mathrm{1} \\ $$$$\Rightarrow{LHS}\:\mathrm{must}\:\mathrm{equal}\:\frac{{x}}{{x}}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\therefore\mathrm{if}\:{a}^{\mathrm{2}} =\mathrm{2}^{{a}} ={u},\:\mathrm{then}:\:\frac{\mathrm{1}+\mathrm{3}}{{u}}=\mathrm{1} \\ $$$$\therefore{u}=\mathrm{4} \\ $$$$\: \\ $$$$\mathrm{then},\:\mathrm{you}\:\mathrm{can}\:\mathrm{test}\:\mathrm{you}\:\mathrm{solution} \\ $$$$\: \\ $$$$\therefore{a}^{\mathrm{2}} =\mathrm{4},\:\:{a}=\pm\mathrm{2} \\ $$$$\: \\ $$$$\mathrm{2}^{{a}} =\mathrm{4},\:\:\:\therefore{a}=\mathrm{2}\:\:\:\:\:\:{a}\neq−\mathrm{2} \\ $$$$\: \\ $$$$\therefore{a}=\mathrm{2} \\ $$
