Question Number 21662 by x² – y²@gmail.com last updated on 30/Sep/17
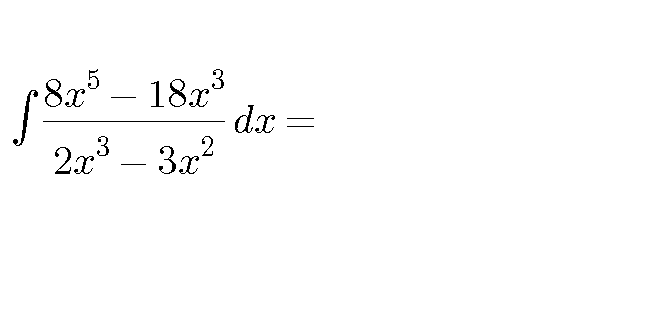
Answered by Joel577 last updated on 30/Sep/17
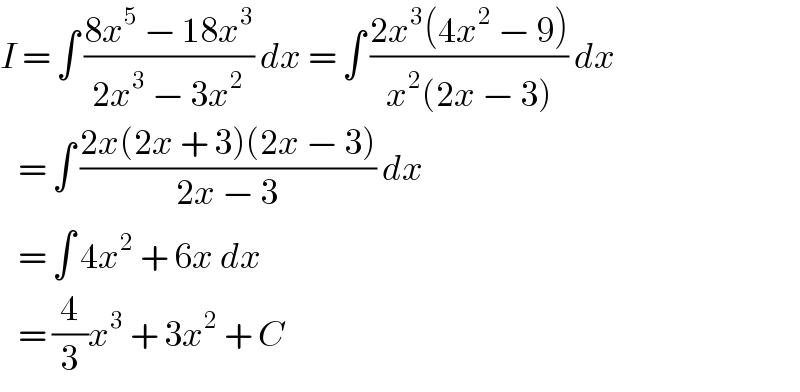
$${I}\:=\:\int\:\frac{\mathrm{8}{x}^{\mathrm{5}} \:−\:\mathrm{18}{x}^{\mathrm{3}} }{\mathrm{2}{x}^{\mathrm{3}} \:−\:\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:=\:\int\:\frac{\mathrm{2}{x}^{\mathrm{3}} \left(\mathrm{4}{x}^{\mathrm{2}} \:−\:\mathrm{9}\right)}{{x}^{\mathrm{2}} \left(\mathrm{2}{x}\:−\:\mathrm{3}\right)}\:{dx} \\ $$$$\:\:\:=\:\int\:\frac{\mathrm{2}{x}\left(\mathrm{2}{x}\:+\:\mathrm{3}\right)\left(\mathrm{2}{x}\:−\:\mathrm{3}\right)}{\mathrm{2}{x}\:−\:\mathrm{3}}\:{dx} \\ $$$$\:\:\:=\:\int\:\mathrm{4}{x}^{\mathrm{2}} \:+\:\mathrm{6}{x}\:{dx} \\ $$$$\:\:\:=\:\frac{\mathrm{4}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\:\mathrm{3}{x}^{\mathrm{2}} \:+\:{C} \\ $$
