Question Number 21722 by mondodotto@gmail.com last updated on 02/Oct/17
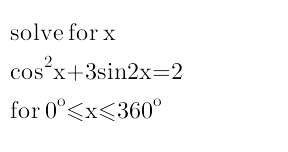
Answered by mrW1 last updated on 02/Oct/17
![cos^2 x+3sin 2x=2 2cos^2 x+6sin 2x=4 2cos^2 x−1+6sin 2x=3 cos 2x+6sin 2x=3 (1/( (√(37))))cos 2x+(6/( (√(37))))sin 2x=(3/( (√(37)))) cos α cos 2x+sin α sin 2x=(3/( (√(37)))) with α=cos^(−1) (1/( (√(37)))) cos (2x−α)=(3/( (√(37)))) ⇒2x−α=2nπ±cos^(−1) (3/( (√(37)))) ⇒x=nπ+(1/2)(α±cos^(−1) (3/( (√(37))))) ⇒x=nπ+(1/2)(cos^(−1) (1/( (√(37))))±cos^(−1) (3/( (√(37))))) in range [0,2π] x=(1/2)(cos^(−1) (1/( (√(37))))−cos^(−1) (3/( (√(37)))))≈10.04° x=(1/2)(cos^(−1) (1/( (√(37))))+cos^(−1) (3/( (√(37)))))≈70.49° x=π+(1/2)(cos^(−1) (1/( (√(37))))−cos^(−1) (3/( (√(37)))))≈190.04° x=π+(1/2)(cos^(−1) (1/( (√(37))))+cos^(−1) (3/( (√(37)))))≈250.49°](https://www.tinkutara.com/question/Q21736.png)
$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}+\mathrm{3sin}\:\mathrm{2x}=\mathrm{2} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\mathrm{x}+\mathrm{6sin}\:\mathrm{2x}=\mathrm{4} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\mathrm{x}−\mathrm{1}+\mathrm{6sin}\:\mathrm{2x}=\mathrm{3} \\ $$$$\mathrm{cos}\:\mathrm{2x}+\mathrm{6sin}\:\mathrm{2x}=\mathrm{3} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\mathrm{cos}\:\mathrm{2x}+\frac{\mathrm{6}}{\:\sqrt{\mathrm{37}}}\mathrm{sin}\:\mathrm{2x}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}} \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:\mathrm{2x}+\mathrm{sin}\:\alpha\:\mathrm{sin}\:\mathrm{2x}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}} \\ $$$$\mathrm{with}\:\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}} \\ $$$$\mathrm{cos}\:\left(\mathrm{2x}−\alpha\right)=\frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}} \\ $$$$\Rightarrow\mathrm{2x}−\alpha=\mathrm{2n}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{n}\pi+\frac{\mathrm{1}}{\mathrm{2}}\left(\alpha\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{n}\pi+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right) \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{range}\:\left[\mathrm{0},\mathrm{2}\pi\right] \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right)\approx\mathrm{10}.\mathrm{04}° \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right)\approx\mathrm{70}.\mathrm{49}° \\ $$$$\mathrm{x}=\pi+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right)\approx\mathrm{190}.\mathrm{04}° \\ $$$$\mathrm{x}=\pi+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\:\sqrt{\mathrm{37}}}\right)\approx\mathrm{250}.\mathrm{49}° \\ $$
Commented by mondodotto@gmail.com last updated on 02/Oct/17
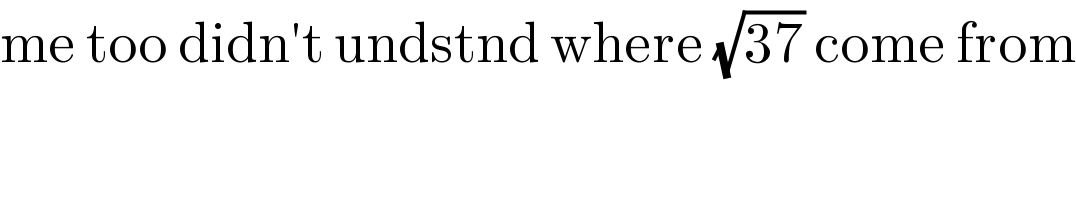
$$\mathrm{me}\:\mathrm{too}\:\mathrm{didn}'\mathrm{t}\:\mathrm{undstnd}\:\mathrm{where}\:\sqrt{\mathrm{37}}\:\mathrm{come}\:\mathrm{from} \\ $$
Commented by mrW1 last updated on 02/Oct/17
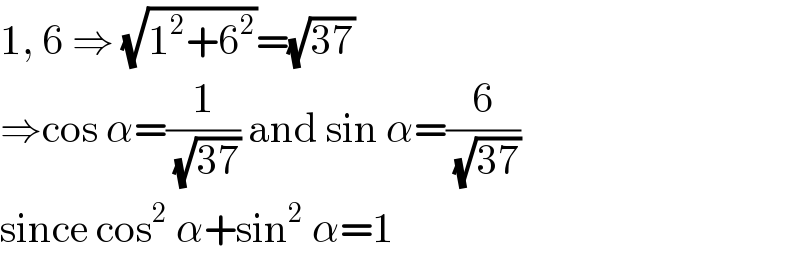
$$\mathrm{1},\:\mathrm{6}\:\Rightarrow\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }=\sqrt{\mathrm{37}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\:\mathrm{and}\:\mathrm{sin}\:\alpha=\frac{\mathrm{6}}{\:\sqrt{\mathrm{37}}} \\ $$$$\mathrm{since}\:\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{1} \\ $$
Commented by Joel577 last updated on 02/Oct/17

$${understood}.\:{thanks} \\ $$
Commented by Joel577 last updated on 02/Oct/17
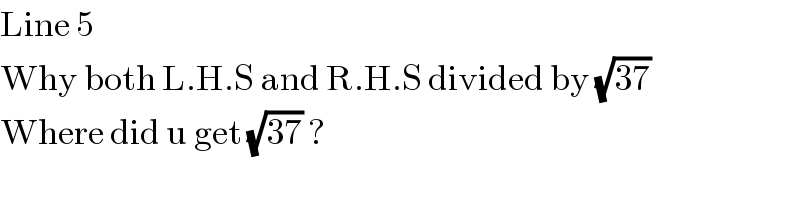
$$\mathrm{Line}\:\mathrm{5} \\ $$$$\mathrm{Why}\:\mathrm{both}\:\mathrm{L}.\mathrm{H}.\mathrm{S}\:\mathrm{and}\:\mathrm{R}.\mathrm{H}.\mathrm{S}\:\mathrm{divided}\:\mathrm{by}\:\sqrt{\mathrm{37}} \\ $$$$\mathrm{Where}\:\mathrm{did}\:\mathrm{u}\:\mathrm{get}\:\sqrt{\mathrm{37}}\:? \\ $$
