Question Number 22116 by ajfour last updated on 11/Oct/17
Commented by ajfour last updated on 11/Oct/17
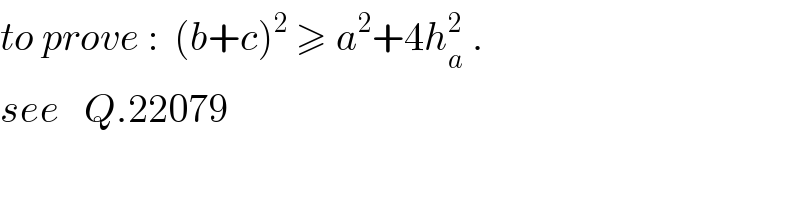
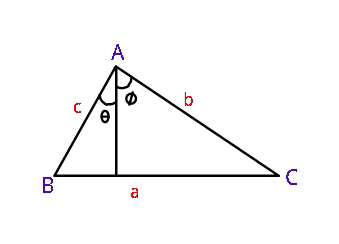
$${to}\:{prove}\::\:\:\left({b}+{c}\right)^{\mathrm{2}} \:\geqslant\:{a}^{\mathrm{2}} +\mathrm{4}{h}_{{a}} ^{\mathrm{2}} \:. \\ $$$${see}\:\:\:{Q}.\mathrm{22079}\:\: \\ $$
Answered by ajfour last updated on 11/Oct/17
![a^2 =b^2 +c^2 −2bc cos (θ+φ) =(b+c)^2 −2bc[1+cos (θ+φ)] =(b+c)^2 −2bc[1+2cos θcos φ −cos θcos φ −sin θsin φ] =(b+c)^2 −2bc[1+2×(h_a /c).(h_a /b)−cos (θ−φ)] =(b+c)^2 −4h_a ^2 −2bc[1−cos (θ−φ)] so (b+c)^2 −a^2 −4h_a ^2 =4bcsin^2 (((θ−φ)/2))≥0 .](https://www.tinkutara.com/question/Q22118.png)
$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$$=\left({b}+{c}\right)^{\mathrm{2}} −\mathrm{2}{bc}\left[\mathrm{1}+\mathrm{cos}\:\left(\theta+\phi\right)\right] \\ $$$$=\left({b}+{c}\right)^{\mathrm{2}} −\mathrm{2}{bc}\left[\mathrm{1}+\mathrm{2cos}\:\theta\mathrm{cos}\:\phi\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{cos}\:\theta\mathrm{cos}\:\phi\:−\mathrm{sin}\:\theta\mathrm{sin}\:\phi\right] \\ $$$$=\left({b}+{c}\right)^{\mathrm{2}} −\mathrm{2}{bc}\left[\mathrm{1}+\mathrm{2}×\frac{{h}_{{a}} }{{c}}.\frac{{h}_{{a}} }{{b}}−\mathrm{cos}\:\left(\theta−\phi\right)\right] \\ $$$$=\left({b}+{c}\right)^{\mathrm{2}} −\mathrm{4}{h}_{{a}} ^{\mathrm{2}} −\mathrm{2}{bc}\left[\mathrm{1}−\mathrm{cos}\:\left(\theta−\phi\right)\right] \\ $$$${so} \\ $$$$\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{4}{h}_{{a}} ^{\mathrm{2}} =\mathrm{4}{bc}\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\theta−\phi}{\mathrm{2}}\right)\geqslant\mathrm{0}\:. \\ $$
Commented by Tinkutara last updated on 11/Oct/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
