Question-22165

Question Number 22165 by A1B1C1D1 last updated on 12/Oct/17

Answered by ajfour last updated on 13/Oct/17

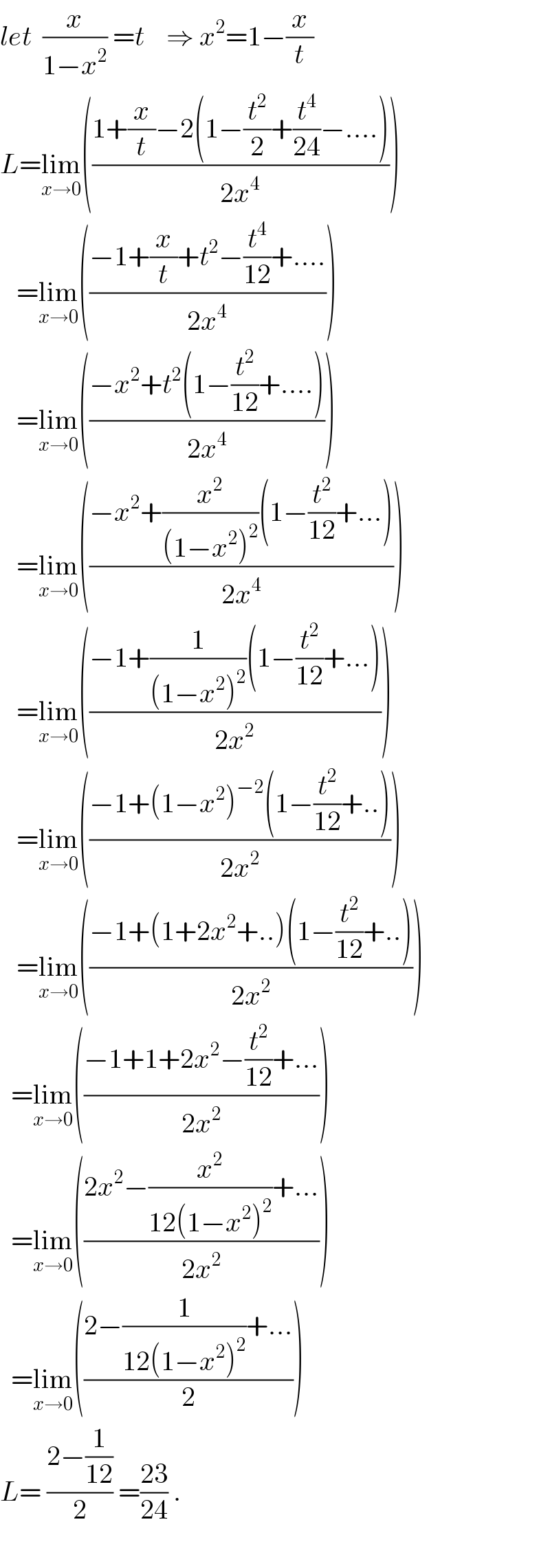
let (x/(1−x^2 )) =t ⇒ x^2 =1−(x/t) L=lim_(x→0) (((1+(x/t)−2(1−(t^2 /2)+(t^4 /(24))−....))/(2x^4 ))) =lim_(x→0) (((−1+(x/t)+t^2 −(t^4 /(12))+....)/(2x^4 ))) =lim_(x→0) (((−x^2 +t^2 (1−(t^2 /(12))+....))/(2x^4 ))) =lim_(x→0) (((−x^2 +(x^2 /((1−x^2 )^2 ))(1−(t^2 /(12))+...))/(2x^4 ))) =lim_(x→0) (((−1+(1/((1−x^2 )^2 ))(1−(t^2 /(12))+...))/(2x^2 ))) =lim_(x→0) (((−1+(1−x^2 )^(−2) (1−(t^2 /(12))+..))/(2x^2 ))) =lim_(x→0) (((−1+(1+2x^2 +..)(1−(t^2 /(12))+..))/(2x^2 ))) =lim_(x→0) (((−1+1+2x^2 −(t^2 /(12))+...)/(2x^2 ))) =lim_(x→0) (((2x^2 −(x^2 /(12(1−x^2 )^2 ))+...)/(2x^2 ))) =lim_(x→0) (((2−(1/(12(1−x^2 )^2 ))+...)/2)) L= ((2−(1/(12)))/2) =((23)/(24)) .

$${let}\:\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:={t}\:\:\:\:\Rightarrow\:{x}^{\mathrm{2}} =\mathrm{1}−\frac{{x}}{{t}} \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+\frac{{x}}{{t}}−\mathrm{2}\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{{t}^{\mathrm{4}} }{\mathrm{24}}−….\right)}{\mathrm{2}{x}^{\mathrm{4}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{1}+\frac{{x}}{{t}}+{t}^{\mathrm{2}} −\frac{{t}^{\mathrm{4}} }{\mathrm{12}}+….}{\mathrm{2}{x}^{\mathrm{4}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−{x}^{\mathrm{2}} +{t}^{\mathrm{2}} \left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+….\right)}{\mathrm{2}{x}^{\mathrm{4}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+…\right)}{\mathrm{2}{x}^{\mathrm{4}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+…\right)}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{1}+\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\mathrm{2}} \left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+..\right)}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{1}+\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} +..\right)\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+..\right)}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{1}+\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} −\frac{{t}^{\mathrm{2}} }{\mathrm{12}}+…}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{12}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+…}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{12}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+…}{\mathrm{2}}\right) \\ $$$${L}=\:\frac{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{12}}}{\mathrm{2}}\:=\frac{\mathrm{23}}{\mathrm{24}}\:. \\ $$$$ \\ $$

Commented by A1B1C1D1 last updated on 13/Oct/17

$$\mathrm{Thank}\:\mathrm{you}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply