Question Number 22313 by math solver last updated on 15/Oct/17
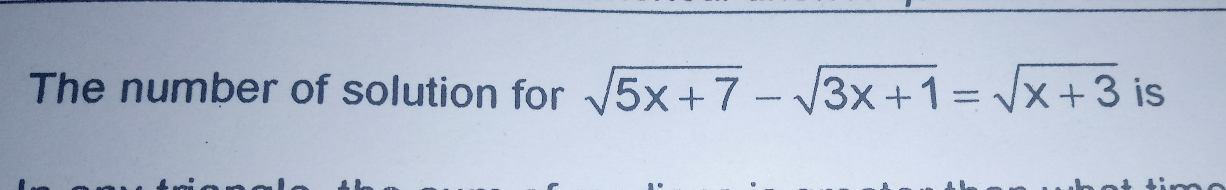
Commented by Joel577 last updated on 16/Oct/17

$$\sqrt{\mathrm{5}{x}\:+\:\mathrm{7}}\:−\:\sqrt{\mathrm{3}{x}\:+\:\mathrm{1}}\:=\:\sqrt{{x}\:+\:\mathrm{3}} \\ $$$${x}\:\geqslant\:−\frac{\mathrm{7}}{\mathrm{5}}\:\:\mathrm{and}\:\:{x}\:\geqslant\:−\frac{\mathrm{1}}{\mathrm{3}}\:\:\mathrm{and}\:\:{x}\:\geqslant\:−\mathrm{3} \\ $$$$\Rightarrow\:{x}\:\geqslant\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$$\left(\sqrt{\mathrm{5}{x}\:+\:\mathrm{7}}\:−\:\sqrt{\mathrm{3}{x}\:+\:\mathrm{1}}\right)^{\mathrm{2}} \:=\:{x}\:+\:\mathrm{3} \\ $$$$\mathrm{5}{x}\:+\:\mathrm{7}\:−\:\mathrm{2}\sqrt{\left(\mathrm{5}{x}\:+\:\mathrm{7}\right)\left(\mathrm{3}{x}\:+\mathrm{1}\right)}\:+\:\mathrm{3}{x}\:+\mathrm{1}\:=\:{x}\:+\:\mathrm{3} \\ $$$$\mathrm{7}{x}\:+\:\mathrm{5}\:−\:\mathrm{2}\sqrt{\left(\mathrm{5}{x}\:+\:\mathrm{7}\right)\left(\mathrm{3}{x}\:+\mathrm{1}\right)}\:=\:\mathrm{0} \\ $$$$\mathrm{7}{x}\:+\:\mathrm{5}\:=\:\mathrm{2}\sqrt{\left(\mathrm{5}{x}\:+\:\mathrm{7}\right)\left(\mathrm{3}{x}\:+\:\mathrm{1}\right)} \\ $$$$\mathrm{49}{x}^{\mathrm{2}} \:+\:\mathrm{70}{x}\:+\:\mathrm{25}\:=\:\mathrm{60}{x}^{\mathrm{2}} \:+\:\mathrm{104}{x}\:+\:\mathrm{28} \\ $$$$\:\:\mathrm{11}{x}^{\mathrm{2}} \:+\:\mathrm{34}{x}\:\:+\:\mathrm{3}\:=\:\mathrm{0} \\ $$$${x}_{\mathrm{1}} \:=\:−\mathrm{3} \\ $$$${x}_{\mathrm{2}} \:=\:−\frac{\mathrm{1}}{\mathrm{11}} \\ $$$$ \\ $$$$\mathrm{Hence},\:\mathrm{the}\:\mathrm{solution}\:\mathrm{that}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{above}\:\mathrm{is}\:\:\left\{−\frac{\mathrm{1}}{\mathrm{11}}\right\} \\ $$
Commented by math solver last updated on 16/Oct/17

$$\left.{thanks}:\right)! \\ $$
Answered by squidward last updated on 16/Oct/17

$${it}\:{is}\:{a}\:{quadratic}\:{equation},\:{hence} \\ $$$${there}\:{are}\:\mathrm{2}\:{solutions} \\ $$
Commented by squidward last updated on 16/Oct/17

$${you}\:{square}\:{both}\:{sides},\:{then}\:{you} \\ $$$${rearrange}\:{and}\:{square}\:{both}\:{sides}\:{again} \\ $$$${it}\:{will}\:{be}\:{a}\:{quadratic}.\: \\ $$
Commented by math solver last updated on 16/Oct/17
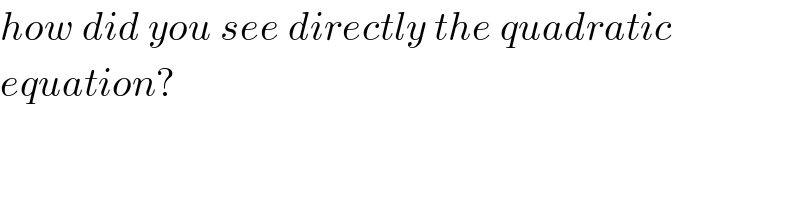
$${how}\:{did}\:{you}\:{see}\:{directly}\:{the}\:{quadratic}\: \\ $$$${equation}? \\ $$
Commented by ajfour last updated on 16/Oct/17

$${if}\:{you}\:{square}\:{you}'{ll}\:{have}\:{to}\:{see} \\ $$$${if}\:{an}\:{obtained}\:{root}\:{is}\:{acceptable} \\ $$$${or}\:{not}. \\ $$
Commented by math solver last updated on 16/Oct/17
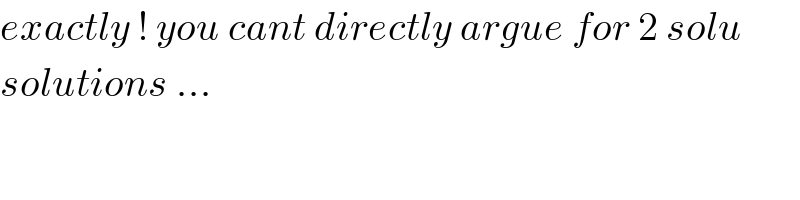
$${exactly}\:!\:{you}\:{cant}\:{directly}\:{argue}\:{for}\:\mathrm{2}\:{solu} \\ $$$${solutions}\:… \\ $$
Commented by squidward last updated on 17/Oct/17

$${yes}\:{i}\:{can}.\:{it}\:{wasnt}\:{specified}\:{if}\:{the} \\ $$$${solutions}\:{have}\:{to}\:{be}\:{real}.\:{hence}\:{there} \\ $$$${are}\:{exactly}\:\mathrm{2}\:{solutions}\:{either}\:{imaginary} \\ $$$${or}\:{not} \\ $$
Commented by math solver last updated on 17/Oct/17
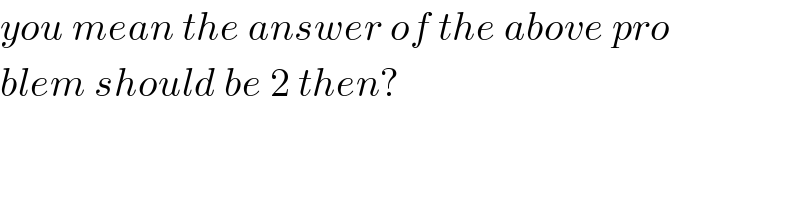
$${you}\:{mean}\:{the}\:{answer}\:{of}\:{the}\:{above}\:{pro} \\ $$$${blem}\:{should}\:{be}\:\mathrm{2}\:{then}? \\ $$
Commented by squidward last updated on 17/Oct/17
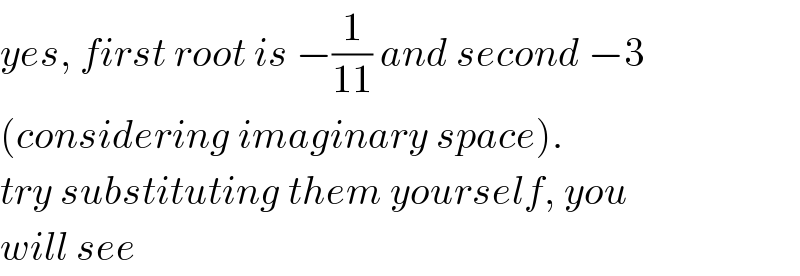
$${yes},\:{first}\:{root}\:{is}\:−\frac{\mathrm{1}}{\mathrm{11}}\:{and}\:{second}\:−\mathrm{3} \\ $$$$\left({considering}\:{imaginary}\:{space}\right).\: \\ $$$${try}\:{substituting}\:{them}\:{yourself},\:{you} \\ $$$${will}\:{see} \\ $$
