Menu Close

Question-22567

Tinku Tara 0 Comments
Pin




Question Number 22567 by mondodotto@gmail.com last updated on 20/Oct/17
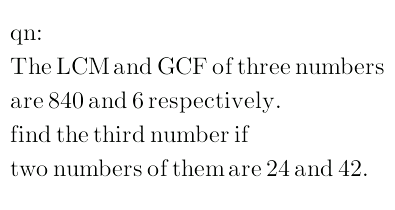
Answered by Rasheed.Sindhi last updated on 20/Oct/17
840=2^3 .3.5.7 ∴ The numbers (of which 840 is lcm) may have factors 2,3,5,7 all or some of them. Suppose the third number is (say y) 2^a .3^b .5^c .7^d with the possibility that some of a,b,c,d may equal to 0. 24=2^3 .3 , 42=2.3.7 , y=2^a .3^b .5^c .7^d HCF =2^(min(3,1,a)) .3^(min(1,b)) .5^0 .7^0 =2^1 .3^1 min(1,a)=1⇒a≥1..............(i) min(1,b)=1⇒b≥1.............(ii) LCM =2^(max(3,1,a)) .3^(max(1,b)) .5^(max(0,c)) .7^(max(0,1,d)) =2^3 .3.5.7 max(3,1,a)=3⇒a≤3..............(iii) max(1,b)=1⇒b≤1..................(iv) max(0,c)=1⇒c=1...................(v) max(0,1,d)=1⇒d≤1.............(vi) (i)&(iii): a≥1∧ a≤3⇒a=1,2,3 (ii)&(iv): b≥1∧b≤1⇒b=1 (v): c=1 (vi):d≤1^ ⇒d=0,1 Hence the third number is 2^(1,2,3) .3^1 .5^1 .7^(0,1) 2^1 .3.5.7^0 =30 2^1 .3.5.7^1 =210 2^2 .3.5.7^0 =60 2^2 .3.5.7^1 =420 2^3 .3.5.7^0 =120 2^3 .3.5.7^1 =840
$$\mathrm{840}=\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7} \\ $$$$\therefore\:\mathrm{The}\:\mathrm{numbers}\:\left(\mathrm{of}\:\mathrm{which}\:\mathrm{840}\:\mathrm{is}\:\mathrm{lcm}\right) \\ $$$$\mathrm{may}\:\mathrm{have}\:\mathrm{factors}\:\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7}\:\mathrm{all}\:\mathrm{or}\:\mathrm{some} \\ $$$$\mathrm{of}\:\mathrm{them}. \\ $$$$\mathrm{Suppose}\:\mathrm{the}\:\mathrm{third}\:\mathrm{number}\:\mathrm{is}\:\left(\mathrm{say}\:\mathrm{y}\right)\: \\ $$$$\:\mathrm{2}^{\mathrm{a}} .\mathrm{3}^{\mathrm{b}} .\mathrm{5}^{\mathrm{c}} .\mathrm{7}^{\mathrm{d}} \:\mathrm{with}\:\mathrm{the}\:\mathrm{possibility}\:\mathrm{that}\: \\ $$$$\mathrm{some}\:\mathrm{of}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{may}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{0}. \\ $$$$\mathrm{24}=\mathrm{2}^{\mathrm{3}} .\mathrm{3}\:,\:\mathrm{42}=\mathrm{2}.\mathrm{3}.\mathrm{7}\:,\:\mathrm{y}=\mathrm{2}^{\mathrm{a}} .\mathrm{3}^{\mathrm{b}} .\mathrm{5}^{\mathrm{c}} .\mathrm{7}^{\mathrm{d}} \\ $$$$\mathrm{HCF} \\ $$$$\:=\mathrm{2}^{\mathrm{min}\left(\mathrm{3},\mathrm{1},\mathrm{a}\right)} .\mathrm{3}^{\mathrm{min}\left(\mathrm{1},\mathrm{b}\right)} .\mathrm{5}^{\mathrm{0}} .\mathrm{7}^{\mathrm{0}} =\mathrm{2}^{\mathrm{1}} .\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{min}\left(\mathrm{1},\mathrm{a}\right)=\mathrm{1}\Rightarrow\mathrm{a}\geqslant\mathrm{1}…………..\left(\mathrm{i}\right) \\ $$$$\mathrm{min}\left(\mathrm{1},\mathrm{b}\right)=\mathrm{1}\Rightarrow\mathrm{b}\geqslant\mathrm{1}………….\left(\mathrm{ii}\right) \\ $$$$\mathrm{LCM} \\ $$$$\:\:=\mathrm{2}^{\mathrm{max}\left(\mathrm{3},\mathrm{1},\mathrm{a}\right)} .\mathrm{3}^{\mathrm{max}\left(\mathrm{1},\mathrm{b}\right)} .\mathrm{5}^{\mathrm{max}\left(\mathrm{0},\mathrm{c}\right)} .\mathrm{7}^{\mathrm{max}\left(\mathrm{0},\mathrm{1},\mathrm{d}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7} \\ $$$$\mathrm{max}\left(\mathrm{3},\mathrm{1},\mathrm{a}\right)=\mathrm{3}\Rightarrow\mathrm{a}\leqslant\mathrm{3}…………..\left(\mathrm{iii}\right) \\ $$$$\mathrm{max}\left(\mathrm{1},\mathrm{b}\right)=\mathrm{1}\Rightarrow\mathrm{b}\leqslant\mathrm{1}………………\left(\mathrm{iv}\right) \\ $$$$\mathrm{max}\left(\mathrm{0},\mathrm{c}\right)=\mathrm{1}\Rightarrow\mathrm{c}=\mathrm{1}……………….\left(\mathrm{v}\right) \\ $$$$\mathrm{max}\left(\mathrm{0},\mathrm{1},\mathrm{d}\right)=\mathrm{1}\Rightarrow\mathrm{d}\leqslant\mathrm{1}………….\left(\mathrm{vi}\right) \\ $$$$\left(\mathrm{i}\right)\&\left(\mathrm{iii}\right):\:\mathrm{a}\geqslant\mathrm{1}\wedge\:\mathrm{a}\leqslant\mathrm{3}\Rightarrow\mathrm{a}=\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$$\left(\mathrm{ii}\right)\&\left(\mathrm{iv}\right):\:\mathrm{b}\geqslant\mathrm{1}\wedge\mathrm{b}\leqslant\mathrm{1}\Rightarrow\mathrm{b}=\mathrm{1} \\ $$$$\left(\mathrm{v}\right):\:\mathrm{c}=\mathrm{1} \\ $$$$\left(\mathrm{vi}\right):\mathrm{d}\leqslant\mathrm{1}^{} \Rightarrow\mathrm{d}=\mathrm{0},\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{third}\:\mathrm{number}\:\mathrm{is} \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{1},\mathrm{2},\mathrm{3}} .\mathrm{3}^{\mathrm{1}} .\mathrm{5}^{\mathrm{1}} .\mathrm{7}^{\mathrm{0},\mathrm{1}} \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{1}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} \:=\mathrm{30}\: \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{1}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{210}\:\: \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} =\mathrm{60}\:\: \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{420}\:\: \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} =\mathrm{120}\:\: \\ $$$$\:\:\:\:\:\:\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{840}\: \\ $$
Answered by Rasheed.Sindhi last updated on 22/Oct/17
A simple approach Let the third number is y. ((24)/6)×((42)/6)×(y/6)×6=840 y=30 The lowest answer. Other answers are such multiples of this which assure the following (i) lcm(24,42,y)=840 and (ii) gcd(24,42,y)=6
$$\mathrm{A}\:\mathrm{simple}\:\mathrm{approach} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{third}\:\mathrm{number}\:\mathrm{is}\:\mathrm{y}. \\ $$$$\frac{\mathrm{24}}{\mathrm{6}}×\frac{\mathrm{42}}{\mathrm{6}}×\frac{\mathrm{y}}{\mathrm{6}}×\mathrm{6}=\mathrm{840} \\ $$$$\mathrm{y}=\mathrm{30}\: \\ $$$$\mathrm{The}\:\mathrm{lowest}\:\mathrm{answer}.\:\mathrm{Other}\:\mathrm{answers} \\ $$$$\mathrm{are}\:\mathrm{such}\:\mathrm{multiples}\:\mathrm{of}\:\mathrm{this}\:\mathrm{which} \\ $$$$\mathrm{assure}\:\mathrm{the}\:\mathrm{following} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{lcm}\left(\mathrm{24},\mathrm{42},\mathrm{y}\right)=\mathrm{840}\:\: \\ $$$$\mathrm{and} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{gcd}\left(\mathrm{24},\mathrm{42},\mathrm{y}\right)=\mathrm{6} \\ $$
Answered by Rasheed.Sindhi last updated on 23/Oct/17
An other simple approach lcm=840 and gcd=6 Let the third is t lcm(24 , 42 , t)=840 lcm(2^3 .3 , 2.3.7 , 2^a .3^b .5^c .7^d )=2^3 .3^ .5.7 a≤3,b≤1,c=1,d≤1...............(i) gcd(2^3 .3 , 2.3.7 , 2^a .3^b .5^c .7^d )=2.3 a≥1,b≥1,c≥0,d≥0...............(ii) (i)&(ii):1≤a≤3 , b=1 , c=1 , d≤1 a=1,2,3 ; b=1 ; c=1 ; d≤1 t=2^(1,2,3) .3.5.7^(0,1) =2^1 .3.5.7^0 =30 =2^1 .3.5.7^1 =210 =2^2 .3.5.7^0 =60 =2^2 .3.5.7^1 =420 =2^3 .3.5.7^0 =120 =2^3 .3.5.7^1 =840
$$\mathrm{An}\:\mathrm{other}\:\mathrm{simple}\:\mathrm{approach} \\ $$$$\:\:\mathrm{lcm}=\mathrm{840}\:\mathrm{and}\:\mathrm{gcd}=\mathrm{6} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{third}\:\mathrm{is}\:\:\mathrm{t} \\ $$$$\:\mathrm{lcm}\left(\mathrm{24}\:\:,\:\:\mathrm{42}\:\:,\:\:\mathrm{t}\right)=\mathrm{840} \\ $$$$\:\mathrm{lcm}\left(\mathrm{2}^{\mathrm{3}} .\mathrm{3}\:\:,\:\:\mathrm{2}.\mathrm{3}.\mathrm{7}\:\:,\:\:\mathrm{2}^{\mathrm{a}} .\mathrm{3}^{\mathrm{b}} .\mathrm{5}^{\mathrm{c}} .\mathrm{7}^{\mathrm{d}} \right)=\mathrm{2}^{\mathrm{3}} .\mathrm{3}^{} .\mathrm{5}.\mathrm{7} \\ $$$$\:\:\mathrm{a}\leqslant\mathrm{3},\mathrm{b}\leqslant\mathrm{1},\mathrm{c}=\mathrm{1},\mathrm{d}\leqslant\mathrm{1}……………\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\:\mathrm{gcd}\left(\mathrm{2}^{\mathrm{3}} .\mathrm{3}\:\:,\:\:\mathrm{2}.\mathrm{3}.\mathrm{7}\:\:,\:\:\mathrm{2}^{\mathrm{a}} .\mathrm{3}^{\mathrm{b}} .\mathrm{5}^{\mathrm{c}} .\mathrm{7}^{\mathrm{d}} \right)=\mathrm{2}.\mathrm{3}\:\: \\ $$$$\:\:\mathrm{a}\geqslant\mathrm{1},\mathrm{b}\geqslant\mathrm{1},\mathrm{c}\geqslant\mathrm{0},\mathrm{d}\geqslant\mathrm{0}……………\left(\mathrm{ii}\right) \\ $$$$ \\ $$$$\:\left(\mathrm{i}\right)\&\left(\mathrm{ii}\right):\mathrm{1}\leqslant\mathrm{a}\leqslant\mathrm{3}\:,\:\mathrm{b}=\mathrm{1}\:,\:\mathrm{c}=\mathrm{1}\:,\:\mathrm{d}\leqslant\mathrm{1} \\ $$$$\mathrm{a}=\mathrm{1},\mathrm{2},\mathrm{3}\:;\:\mathrm{b}=\mathrm{1}\:;\:\mathrm{c}=\mathrm{1}\:;\:\mathrm{d}\leqslant\mathrm{1} \\ $$$$\:\mathrm{t}=\mathrm{2}^{\mathrm{1},\mathrm{2},\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0},\mathrm{1}} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{1}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} =\mathrm{30} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{1}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{210} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{2}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} =\mathrm{60} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{2}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{420} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{0}} =\mathrm{120} \\ $$$$\:\:\:=\mathrm{2}^{\mathrm{3}} .\mathrm{3}.\mathrm{5}.\mathrm{7}^{\mathrm{1}} =\mathrm{840} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *