Question Number 22661 by ajfour last updated on 21/Oct/17

Commented by ajfour last updated on 21/Oct/17

$${Q}.\mathrm{22657}\:\left({solution}\:;\:{here}\:\:{becoz}\right. \\ $$$$\:\:\:\:\:\left({images}\:{from}\:{my}\:{cellphone}\right. \\ $$$$\:\:\:\:\:{gets}\:{uploaded}\:{only}\:{as}\:{new}\: \\ $$$$\:\:\:\:\:\:{question},\:{and}\:{rarely}\:{as}\:{ans} \\ $$$$\left.\:\:\:\:\:\:{or}\:{comment}\right). \\ $$
Answered by ajfour last updated on 21/Oct/17
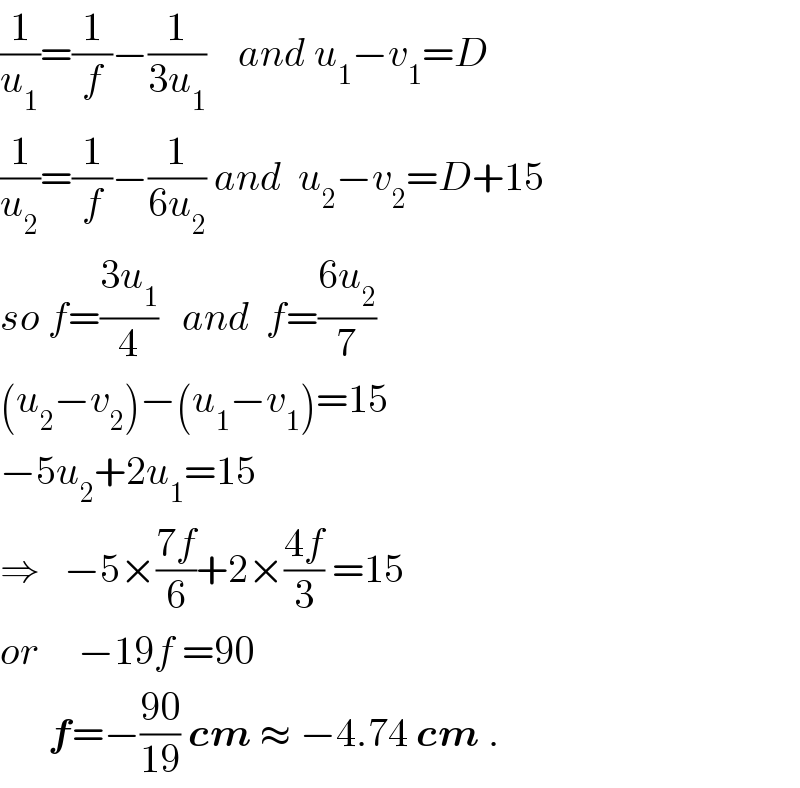
$$\frac{\mathrm{1}}{{u}_{\mathrm{1}} }=\frac{\mathrm{1}}{{f}}−\frac{\mathrm{1}}{\mathrm{3}{u}_{\mathrm{1}} }\:\:\:\:{and}\:{u}_{\mathrm{1}} −{v}_{\mathrm{1}} ={D} \\ $$$$\frac{\mathrm{1}}{{u}_{\mathrm{2}} }=\frac{\mathrm{1}}{{f}}−\frac{\mathrm{1}}{\mathrm{6}{u}_{\mathrm{2}} }\:{and}\:\:{u}_{\mathrm{2}} −{v}_{\mathrm{2}} ={D}+\mathrm{15} \\ $$$${so}\:{f}=\frac{\mathrm{3}{u}_{\mathrm{1}} }{\mathrm{4}}\:\:\:{and}\:\:{f}=\frac{\mathrm{6}{u}_{\mathrm{2}} }{\mathrm{7}} \\ $$$$\left({u}_{\mathrm{2}} −{v}_{\mathrm{2}} \right)−\left({u}_{\mathrm{1}} −{v}_{\mathrm{1}} \right)=\mathrm{15} \\ $$$$−\mathrm{5}{u}_{\mathrm{2}} +\mathrm{2}{u}_{\mathrm{1}} =\mathrm{15} \\ $$$$\Rightarrow\:\:\:−\mathrm{5}×\frac{\mathrm{7}{f}}{\mathrm{6}}+\mathrm{2}×\frac{\mathrm{4}{f}}{\mathrm{3}}\:=\mathrm{15} \\ $$$${or}\:\:\:\:\:−\mathrm{19}{f}\:=\mathrm{90} \\ $$$$\:\:\:\:\:\:\boldsymbol{{f}}=−\frac{\mathrm{90}}{\mathrm{19}}\:\boldsymbol{{cm}}\:\approx\:−\mathrm{4}.\mathrm{74}\:\boldsymbol{{cm}}\:. \\ $$
