Question Number 22692 by Sahib singh last updated on 22/Oct/17

Commented by Sahib singh last updated on 22/Oct/17

$${find}\:{hinge}\:{reaction}\:{at}\:{A} \\ $$$$\&\:{angular}\:{velocity}\:{of}\:{rod}. \\ $$
Answered by ajfour last updated on 22/Oct/17

$${mg}\left(\frac{{l}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right)\omega^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left(\boldsymbol{\omega}\:=\sqrt{\frac{\mathrm{3}\boldsymbol{{g}}}{\boldsymbol{{l}}}}\:\right. \\ $$$$\:{F}_{{H}} \:=\:{mg}+{m}\omega^{\mathrm{2}} \left(\frac{{l}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:={mg}+{m}\left(\mathrm{3}{g}/\mathrm{2}\right)\: \\ $$$$\:\:\:\:\:\boldsymbol{{F}}_{\boldsymbol{{H}}} \:=\frac{\mathrm{5}\boldsymbol{{mg}}}{\mathrm{2}}\:. \\ $$
Commented by Sahib singh last updated on 22/Oct/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$$$\left.\mathrm{you}\:\mathrm{are}\:\mathrm{the}\:\mathrm{best}\::\right) \\ $$
Commented by mrW1 last updated on 22/Oct/17
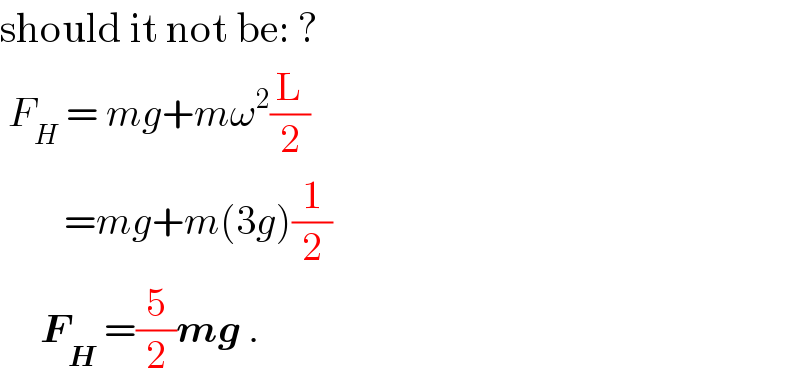
$$\mathrm{should}\:\mathrm{it}\:\mathrm{not}\:\mathrm{be}:\:? \\ $$$$\:{F}_{{H}} \:=\:{mg}+{m}\omega^{\mathrm{2}} \frac{\mathrm{L}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:={mg}+{m}\left(\mathrm{3}{g}\right)\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\:\:\:\:\:\boldsymbol{{F}}_{\boldsymbol{{H}}} \:=\frac{\mathrm{5}}{\mathrm{2}}\boldsymbol{{mg}}\:. \\ $$
Commented by Sahib singh last updated on 22/Oct/17

$$\mathrm{oh}\:!\:\mathrm{yeah},\:\mathrm{MrW1}\:\mathrm{is}\:\mathrm{right} \\ $$
Commented by ajfour last updated on 22/Oct/17

$${yes}\:{sir},\:{thanks}\:{for}\:{supervision}. \\ $$
