Question Number 22729 by selestian last updated on 22/Oct/17

Commented by math solver last updated on 22/Oct/17

$$\mathrm{0} \\ $$
Commented by selestian last updated on 22/Oct/17

$${sir}\:{please}\:{send}\:{me}\:{the}\:{solution} \\ $$
Commented by math solver last updated on 22/Oct/17

$${i}\:{have}\:{sent}.\:{see}\:{below} \\ $$
Commented by math solver last updated on 22/Oct/17
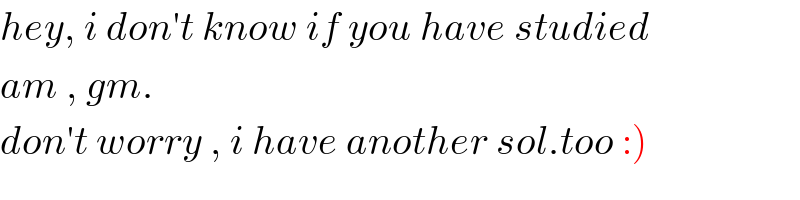
$${hey},\:{i}\:{don}'{t}\:{know}\:{if}\:{you}\:{have}\:{studied} \\ $$$${am}\:,\:{gm}. \\ $$$$\left.{don}'{t}\:{worry}\:,\:{i}\:{have}\:{another}\:{sol}.{too}\::\right) \\ $$
Commented by selestian last updated on 22/Oct/17

$${yes}\:{i}\:{had}\:{studied}\:{am}\:{nd}\:{gm}\:{thanks} \\ $$$$ \\ $$
Answered by math solver last updated on 22/Oct/17

Answered by $@ty@m last updated on 24/Oct/17

$${Let}\:\mathrm{2}^{{x}} ={y} \\ $$$$\Rightarrow\mathrm{sin}\:\left({e}^{{x}} \right)={y}+\frac{\mathrm{1}}{{y}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{sin}\:\left({e}^{{x}} \right){y}+\mathrm{1}=\mathrm{0}\:\:−−−\left(\mathrm{1}\right) \\ $$$${D}={b}^{\mathrm{2}} −\mathrm{4}{ac} \\ $$$$=\mathrm{sin}\:^{\mathrm{2}} \left({e}^{{x}} \right)−\mathrm{4} \\ $$$$\Rightarrow\mathrm{0}−\mathrm{4}\leqslant{D}\leqslant\mathrm{1}−\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\because\mathrm{0}\leqslant\mathrm{sin}\:^{\mathrm{2}} \theta\leqslant\mathrm{1}\right\} \\ $$$$\Rightarrow−\mathrm{4}\leqslant{D}\leqslant−\mathrm{3} \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:{has}\:{no}\:{real}\:{root}. \\ $$
