Question Number 22778 by selestian last updated on 22/Oct/17

Commented by selestian last updated on 22/Oct/17

$${plz}\:{solve}\:{this}\:{i}\:{am}\:{trying}\:{to}\:{do}\:{by} \\ $$$${uing}\:{n}=\mathrm{3}\:{but}\:{its}\:{not}\:{working} \\ $$$$ \\ $$
Commented by mrW1 last updated on 22/Oct/17
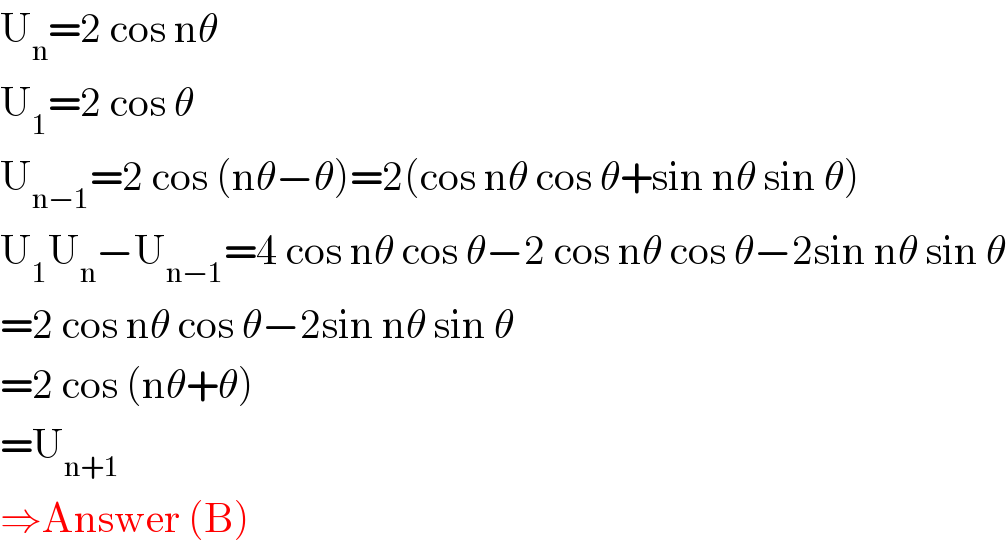
$$\mathrm{U}_{\mathrm{n}} =\mathrm{2}\:\mathrm{cos}\:\mathrm{n}\theta \\ $$$$\mathrm{U}_{\mathrm{1}} =\mathrm{2}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{U}_{\mathrm{n}−\mathrm{1}} =\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{n}\theta−\theta\right)=\mathrm{2}\left(\mathrm{cos}\:\mathrm{n}\theta\:\mathrm{cos}\:\theta+\mathrm{sin}\:\mathrm{n}\theta\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{U}_{\mathrm{1}} \mathrm{U}_{\mathrm{n}} −\mathrm{U}_{\mathrm{n}−\mathrm{1}} =\mathrm{4}\:\mathrm{cos}\:\mathrm{n}\theta\:\mathrm{cos}\:\theta−\mathrm{2}\:\mathrm{cos}\:\mathrm{n}\theta\:\mathrm{cos}\:\theta−\mathrm{2sin}\:\mathrm{n}\theta\:\mathrm{sin}\:\theta \\ $$$$=\mathrm{2}\:\mathrm{cos}\:\mathrm{n}\theta\:\mathrm{cos}\:\theta−\mathrm{2sin}\:\mathrm{n}\theta\:\mathrm{sin}\:\theta \\ $$$$=\mathrm{2}\:\mathrm{cos}\:\left(\mathrm{n}\theta+\theta\right) \\ $$$$=\mathrm{U}_{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{Answer}\:\left(\mathrm{B}\right) \\ $$
