Question Number 22939 by selestian last updated on 24/Oct/17

Answered by ajfour last updated on 24/Oct/17
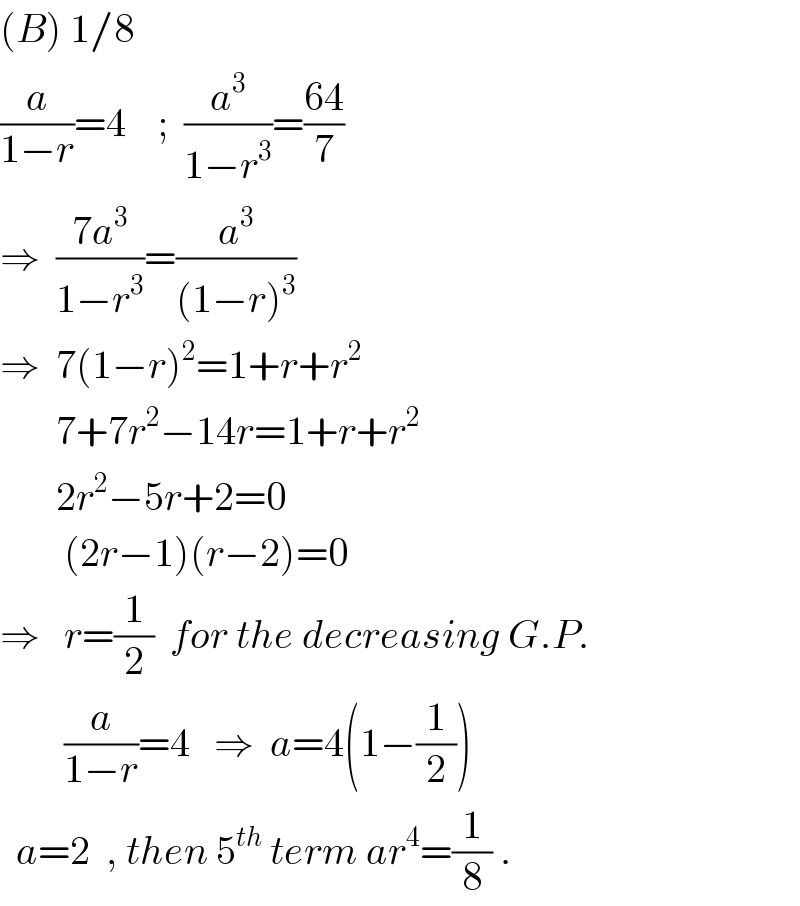
$$\left({B}\right)\:\mathrm{1}/\mathrm{8} \\ $$$$\frac{{a}}{\mathrm{1}−{r}}=\mathrm{4}\:\:\:\:;\:\:\frac{{a}^{\mathrm{3}} }{\mathrm{1}−{r}^{\mathrm{3}} }=\frac{\mathrm{64}}{\mathrm{7}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{7}{a}^{\mathrm{3}} }{\mathrm{1}−{r}^{\mathrm{3}} }=\frac{{a}^{\mathrm{3}} }{\left(\mathrm{1}−{r}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow\:\:\mathrm{7}\left(\mathrm{1}−{r}\right)^{\mathrm{2}} =\mathrm{1}+{r}+{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{7}+\mathrm{7}{r}^{\mathrm{2}} −\mathrm{14}{r}=\mathrm{1}+{r}+{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}{r}^{\mathrm{2}} −\mathrm{5}{r}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{2}{r}−\mathrm{1}\right)\left({r}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}}\:\:{for}\:{the}\:{decreasing}\:{G}.{P}. \\ $$$$\:\:\:\:\:\:\:\:\frac{{a}}{\mathrm{1}−{r}}=\mathrm{4}\:\:\:\Rightarrow\:\:{a}=\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:{a}=\mathrm{2}\:\:,\:{then}\:\mathrm{5}^{{th}} \:{term}\:{ar}^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{8}}\:. \\ $$
