Question-22956

Facebook Tweet Pin

Question Number 22956 by Physics lover last updated on 24/Oct/17

Commented by Physics lover last updated on 24/Oct/17

$${find}\:{angular}\:{velocity}\:{after}\: \\ $$$${collision}\:{and}\:{loss}\:{in}\:{kinetic} \\ $$$${energy}? \\ $$

Commented by ajfour last updated on 24/Oct/17

Commented by ajfour last updated on 24/Oct/17

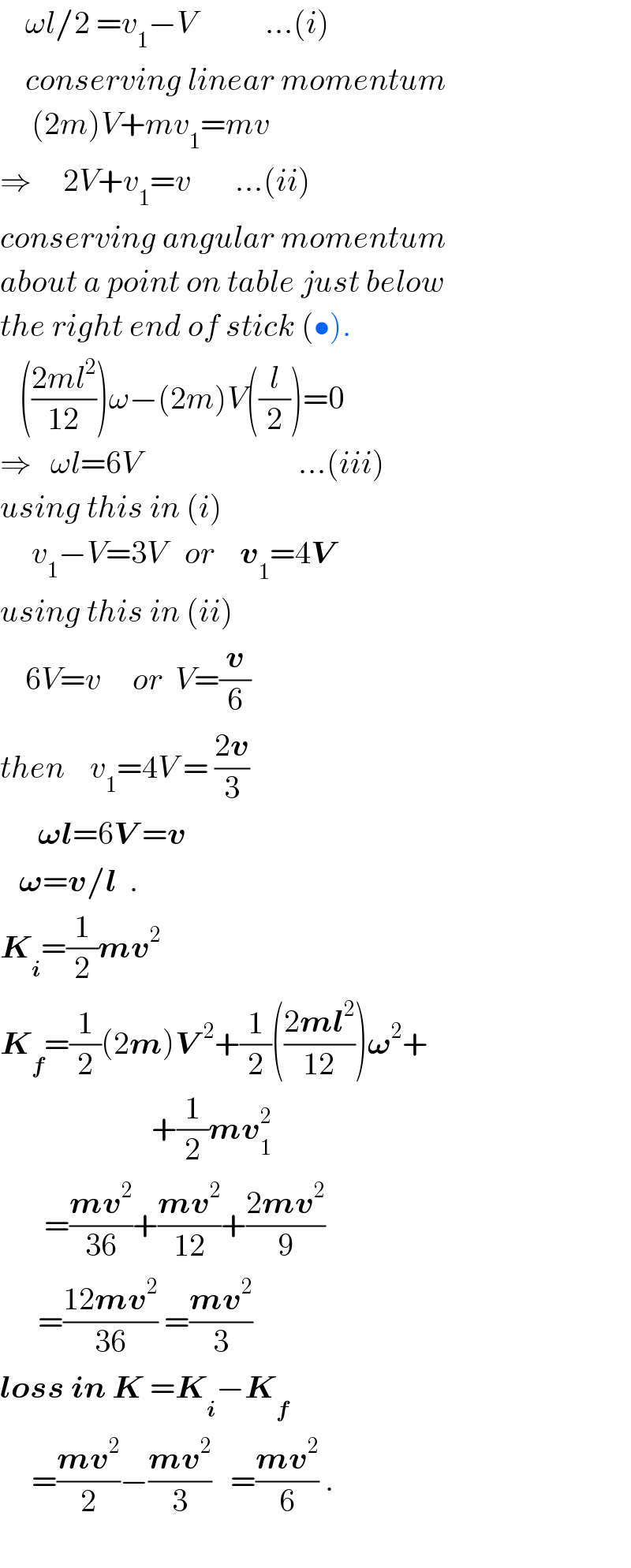
ωl/2 =v_1 −V ...(i) conserving linear momentum (2m)V+mv_1 =mv ⇒ 2V+v_1 =v ...(ii) conserving angular momentum about a point on table just below the right end of stick (•). (((2ml^2 )/(12)))ω−(2m)V((l/2))=0 ⇒ ωl=6V ...(iii) using this in (i) v_1 −V=3V or v_1 =4V using this in (ii) 6V=v or V=(v/6) then v_1 =4V = ((2v)/3) 𝛚l=6V =v 𝛚=v/l . K_i =(1/2)mv^2 K_f =(1/2)(2m)V^( 2) +(1/2)(((2ml^2 )/(12)))𝛚^2 + +(1/2)mv_1 ^2 =((mv^2 )/(36))+((mv^2 )/(12))+((2mv^2 )/9) =((12mv^2 )/(36)) =((mv^2 )/3) loss in K =K_i −K_f =((mv^2 )/2)−((mv^2 )/3) =((mv^2 )/6) .

$$\:\:\:\:\omega{l}/\mathrm{2}\:={v}_{\mathrm{1}} −{V}\:\:\:\:\:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:{conserving}\:{linear}\:{momentum} \\ $$$$\:\:\:\:\:\left(\mathrm{2}{m}\right){V}+{mv}_{\mathrm{1}} ={mv} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{2}{V}+{v}_{\mathrm{1}} ={v}\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$${conserving}\:{angular}\:{momentum} \\ $$$${about}\:{a}\:{point}\:{on}\:{table}\:{just}\:{below} \\ $$$${the}\:{right}\:{end}\:{of}\:{stick}\:\left(\bullet\right). \\ $$$$\:\:\:\left(\frac{\mathrm{2}{ml}^{\mathrm{2}} }{\mathrm{12}}\right)\omega−\left(\mathrm{2}{m}\right){V}\left(\frac{{l}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\omega{l}=\mathrm{6}{V}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$${using}\:{this}\:{in}\:\left({i}\right) \\ $$$$\:\:\:\:\:{v}_{\mathrm{1}} −{V}=\mathrm{3}{V}\:\:\:{or}\:\:\:\:\boldsymbol{{v}}_{\mathrm{1}} =\mathrm{4}\boldsymbol{{V}}\:\: \\ $$$${using}\:{this}\:{in}\:\left({ii}\right) \\ $$$$\:\:\:\:\mathrm{6}{V}={v}\:\:\:\:\:{or}\:\:{V}=\frac{\boldsymbol{{v}}}{\mathrm{6}}\: \\ $$$${then}\:\:\:\:{v}_{\mathrm{1}} =\mathrm{4}{V}\:=\:\frac{\mathrm{2}\boldsymbol{{v}}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\omega{l}}=\mathrm{6}\boldsymbol{{V}}\:=\boldsymbol{{v}} \\ $$$$\:\:\:\boldsymbol{\omega}=\boldsymbol{{v}}/\boldsymbol{{l}}\:\:. \\ $$$$\boldsymbol{{K}}_{\boldsymbol{{i}}} =\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{mv}}^{\mathrm{2}} \\ $$$$\boldsymbol{{K}}_{\boldsymbol{{f}}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\boldsymbol{{m}}\right)\boldsymbol{{V}}^{\:\:\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}\boldsymbol{{ml}}^{\mathrm{2}} }{\mathrm{12}}\right)\boldsymbol{\omega}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{mv}}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{36}}+\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{12}}+\frac{\mathrm{2}\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{12}\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{36}}\:=\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\boldsymbol{{loss}}\:\boldsymbol{{in}}\:\boldsymbol{{K}}\:=\boldsymbol{{K}}_{\boldsymbol{{i}}} −\boldsymbol{{K}}_{\boldsymbol{{f}}} \\ $$$$\:\:\:\:\:=\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{2}}−\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{3}}\:\:\:=\frac{\boldsymbol{{mv}}^{\mathrm{2}} }{\mathrm{6}}\:. \\ $$$$ \\ $$

Commented by Physics lover last updated on 25/Oct/17